Intérêts composés
L’intérêt composé est l’un des concepts les plus importants du monde moderne et une pierre angulaire du système financier de toute économie. Le concept d’« intérêt composé » est étonnamment simple, mais incroyablement puissant !
Intérêts simples
Avant de parler de la puissance de l’intérêt composé, nous devons d’abord comprendre l’intérêt simple.
Dans le monde financier, l’intérêt simple représente le rendement d’un prêt. Par exemple, si votre ami vous demande un emprunt de 100 $ et promet de vous rembourser 110 $ dans un an, vous réaliserez un bénéfice de 10 $ en prêtant cet argent. L’« intérêt » est le taux de rendement, c’est-à-dire le bénéfice réalisé en pourcentage de l’investissement initial. En termes d’investissement, les 100 $ initialement investis constituent le « capital ».

Intérêts = (Remboursement – Capital) / Capital
Dans l’exemple ci-dessus, les intérêts gagnés sont de 10 %.
(110 – 100) / 100 = 10%
Dans le monde financier, l’intérêt est généralement exprimé en rendement annuel. Si votre ami promettait de vous rembourser en six mois, le taux d’intérêt annuel serait ajusté. Puisque six mois représentent la moitié d’une année, le taux d’intérêt annuel est le double du rendement sur six mois.
Intérêt annuel = Intérêts * Durée du prêt, en pourcentage d’un an
Donc, si l’ami rembourse dans 6 mois, l’intérêt annuel sera de 20 %.
Intérêt annuel = 10 % * 2 = 20 %
Donc, si l’on a le choix entre un rendement de 20 % (votre ami remboursant le prêt, plus 10 $, en 6 mois) au lieu d’un rendement de 10 % (un ami attendant 12 mois pour rembourser), le rendement de 20 % est clairement meilleur.
Intérêts simples et obligations
L’investissement obligataire fonctionne sur la base d’un intérêt simple. Une obligation coûte généralement 1 000 $ et comporte un taux d’intérêt et une date d’expiration (généralement 30 ans après son émission).
Si vous achetez une obligation de 1 000 $, elle vous rapportera 50 $ par an pendant 30 ans. À la fin de la 30e année, vous recevrez le dernier versement de 50 $, plus votre capital initial de 1 000 $, soit un simple versement d’intérêt de 5 % par an.

Intérêt simple vs intérêt composé
L’intérêt simple est tout simplement simple. L’intérêt composé est un peu plus complexe en apparence. Avec l’intérêt composé, au lieu de simplement payer les intérêts à la fin du prêt, le montant remboursé est réinvesti.
Reprenons l’exemple de notre ami qui emprunte 100 $. Lorsqu’il nous rembourse dans un an, au moment même où il nous remet les 110 $, il demande à emprunter ces 110 $ pour une année supplémentaire, avec le même taux d’intérêt de 10 %. Cela signifie qu’à la fin de l’année suivante, son « paiement d’intérêts » sera de 110 $ * 10 % = 11 $, soit un montant total remboursé de 121 $.
Comme l’ami a emprunté la totalité du montant, y compris les intérêts de la première année, la récompense est plus importante ! Cela signifie que chaque année, le « remboursement » de chaque prêt s’ajoute au montant initial, « composant » le capital (et les intérêts perçus) l’année suivante.
Exemples d’intérêts composés
L’intérêt composé est couramment utilisé en épargne et en investissement. Un compte d’épargne est un exemple classique d’intérêt composé. Votre banque verse des intérêts sur votre épargne chaque mois, puis ces intérêts sont déposés sur le compte d’épargne lui-même. Ainsi, le mois suivant, vous percevrez des intérêts sur le dépôt initial, plus les intérêts perçus le premier mois.
Investir en bourse est également considéré comme une forme d’intérêt composé. Si la valeur d’un investissement augmente de 10 % chaque année, cela signifie que les rendements de l’année précédente sont inclus dans les gains !
La règle des 72
La règle des 72 Il existe un moyen simple d’estimer le temps nécessaire pour que votre investissement double grâce aux intérêts composés. Il suffit de diviser 72 par le taux d’intérêt annuel (en pourcentage) : cela vous indique précisément le temps nécessaire pour que l’investissement initial double !
| Taux d’intérêt | Il est temps de doubler |
|---|---|
| 1% | 72 Années |
| 2% | 36 Années |
| 5% | 14.4 Années |
| 10% | 7.2 Années |
| 20% | 3.6 Années |
Intérêts composés ou simples – En pratique
Nous avons maintenant vu comment fonctionnent les intérêts simples, avec une obligation, et les intérêts composés, avec un compte d’épargne. Mais pour comprendre l’efficacité des intérêts composés, comparons-les sur 30 ans (la durée d’expiration moyenne d’une obligation) afin d’observer la différence de rendement entre nos deux investissements.
Intérêts simples
| Année | Principale | Intérêts gagnés |
| 1 | $ 1,000 | $50 |
| 2 | $ 1,000 | $50 |
| 3 | $ 1,000 | $50 |
| 4 | $ 1,000 | $50 |
| 5 | $ 1,000 | $50 |
| 6 | $ 1,000 | $50 |
| 7 | $ 1,000 | $50 |
| 8 | $ 1,000 | $50 |
| 9 | $ 1,000 | $50 |
| 10 | $ 1,000 | $50 |
| 11 | $ 1,000 | $50 |
| 12 | $ 1,000 | $50 |
| 13 | $ 1,000 | $50 |
| 14 | $ 1,000 | $50 |
| 15 | $ 1,000 | $50 |
| 16 | $ 1,000 | $50 |
| 17 | $ 1,000 | $50 |
| 18 | $ 1,000 | $50 |
| 19 | $ 1,000 | $50 |
| 20 | $ 1,000 | $50 |
| 21 | $ 1,000 | $50 |
| 22 | $ 1,000 | $50 |
| 23 | $ 1,000 | $50 |
| 24 | $ 1,000 | $50 |
| 25 | $ 1,000 | $50 |
| 26 | $ 1,000 | $50 |
| 27 | $ 1,000 | $50 |
| 28 | $ 1,000 | $50 |
| 29 | $ 1,000 | $50 |
| 30 | $ 1,000 | $50 |
| Totale | $1,500 |
Intérêts composés
| Année | Principale | Intérêts gagnés |
| 1 | $ 1,000 | $ 50 |
| 2 | $ 1,050 | $ 53 |
| 3 | $ 1,103 | $ 55 |
| 4 | $ 1,158 | $ 58 |
| 5 | $ 1,216 | $ 61 |
| 6 | $ 1,276 | $ 64 |
| 7 | $ 1,340 | $ 67 |
| 8 | $ 1,407 | $ 70 |
| 9 | $ 1,477 | $ 74 |
| 10 | $ 1,551 | $ 78 |
| 11 | $ 1,629 | $ 81 |
| 12 | $ 1,710 | $ 86 |
| 13 | $ 1,796 | $ 90 |
| 14 | $ 1,886 | $ 94 |
| 15 | $ 1,980 | $ 99 |
| 16 | $ 2,079 | $ 104 |
| 17 | $ 2,183 | $ 109 |
| 18 | $ 2,292 | $ 115 |
| 19 | $ 2,407 | $ 120 |
| 20 | $ 2,527 | $ 126 |
| 21 | $ 2,653 | $ 133 |
| 22 | $ 2,786 | $ 139 |
| 23 | $ 2,925 | $ 146 |
| 24 | $ 3,072 | $ 154 |
| 25 | $ 3,225 | $ 161 |
| 26 | $ 3,386 | $ 169 |
| 27 | $ 3,556 | $ 178 |
| 28 | $ 3,733 | $ 187 |
| 29 | $ 3,920 | $ 196 |
| 30 | $ 4,116 | $ 206 |
| Totale | $3,322 |
Dans cet exemple, vous pouvez constater que les intérêts composés offrent un rendement total plus de deux fois supérieur à celui des intérêts simples ; c’est un atout considérable ! Si vous observez un graphique de la valeur totale de votre investissement, vous constaterez également une nette différence de forme :
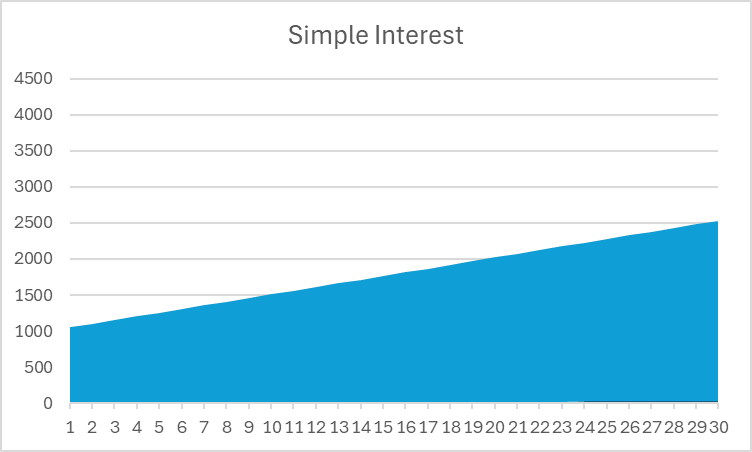
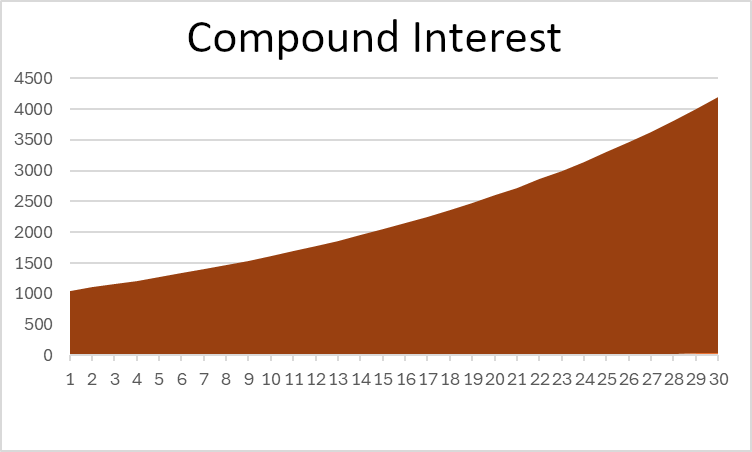
Notez que l’intérêt simple est une ligne droite, tandis que l’intérêt composé suit une courbe ascendante au fil du temps.
Le cas de l’intérêt simple
Même si vous souhaitez absolument que votre épargne soit capitalisée au fil du temps pour obtenir un meilleur rendement à long terme, cela ne signifie pas pour autant qu’il faille négliger l’intérêt simple. Cela signifie simplement que si vous souhaitez que votre épargne soit capitalisée, il vous faudra un peu plus d’efforts.
Prenons l’exemple d’un investissement en obligations. Bien que les obligations versent des intérêts simples, vous pouvez les réinvestir ailleurs (par exemple en les déposant sur un compte d’épargne ou en achetant des obligations), ce qui vous permet d’obtenir des « rendements composés » même s’ils produisent des intérêts simples.
Tant que vous continuez à réinvestir vos rendements (sans les dépenser ni les conserver sous forme de liquidités), vous continuez à les capitaliser !
Fréquence de composition
Un dernier point à prendre en compte concernant les intérêts composés peut compliquer un peu les choses : la fréquence de capitalisation.
Nous avons mentionné précédemment qu’un compte d’épargne verse des intérêts mensuels, même s’il utilise un taux d’intérêt annuel de 5 %. Cela signifie que votre banque versera en réalité 5 % / 12 intérêts chaque mois (soit environ 0,42 %).
Cela signifie que votre compte bancaire est capitalisé à un taux d’intérêt plus faible, mais à une fréquence plus élevée, qu’un autre compte bancaire qui ne verse ses intérêts qu’annuellement. Comme votre compte est capitalisé plus souvent, votre rendement « effectif » est légèrement supérieur : avec un taux d’intérêt de 5 % et 1 000 $ d’épargne, une seule capitalisation rapporterait 1 050 $, mais une capitalisation mensuelle aboutit à environ 1 051,16 $. Ces 1,16 $ supplémentaires ne sont pas énormes, mais ils ne sont pas non plus négligeables.

Formule d’intérêt composé
Grâce à la puissance des Exponents, nous pouvons calculer le solde final d’un investissement à intérêts composés sans avoir à effectuer de calculs manuels chaque année, comme nous l’avons fait précédemment. La formule est la suivante :
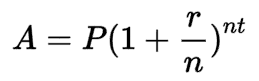
Where:
- A est le solde final
- P est le capital initial
- r est le taux d’intérêt (en finance, généralement un taux annuel)
- n est le nombre de périodes de capitalisation de l’investissement
- t est le nombre de périodes de temps que nous mesurons.
Dans notre exemple de capitalisation annuelle sur 30 ans, P serait de 1 000 $, r de 5 %, n de 1 (une capitalisation par an) et t de 30, sur 30 ans. Si nous calculions les intérêts mensuels, « n » serait plutôt 12, car ils sont capitalisés 12 fois par an.
Vous pouvez observer la différence entre différents types de capitalisation et différents taux d’intérêt en jouant avec notre Calculateur d’intérêts composés !
Return To Glossary