Interés compuesto
El interés compuesto es uno de los conceptos más importantes del mundo moderno y una piedra angular del sistema financiero de toda economía. El concepto de “interés compuesto” es sorprendentemente simple, ¡pero increíblemente poderoso!
Interés simple
Antes de hablar sobre el poder del interés compuesto, primero debemos comprender el interés simple.
En el mundo financiero, el interés simple es la rentabilidad de un préstamo. Por ejemplo, si un amigo te pide prestados $100 y promete devolver $110 dentro de un año, obtendrías una ganancia de $10 al prestarle el dinero. El “interés” es la tasa de rendimiento, o el porcentaje de la ganancia obtenida sobre la inversión original. En términos de inversión, los $100 originales que invertiste se llaman “capital”.

Interés = (Pago – Capital) / Capital
En el ejemplo anterior, el interés ganado es del 10%.
(110 – 100) / 100 = 10%
En el mundo financiero, el interés suele expresarse en la rentabilidad anual. Si, en cambio, tu amigo te prometiera pagarte en 6 meses, la tasa de interés anual se ajustaría. Como 6 meses son la mitad de un año, la tasa de interés anual es el doble de la rentabilidad de 6 meses.
Interés anual = Interés * Duración del préstamo, como porcentaje de 1 año
Entonces, si el amigo paga en 6 meses, el interés anual sería del 20%.
Interés anual = 10% * 2 = 20%.
Por lo tanto, si se pudiera optar por una rentabilidad del 20% (que su amigo devuelva el préstamo, más $10, en 6 meses) en lugar de una rentabilidad del 10% (que su amigo espere 12 meses para pagar), la rentabilidad del 20% es claramente mejor.
Interés simple y bonos
La inversión en bonos funciona con un interés simple. Los bonos suelen costar $1,000 y cada uno tiene una tasa de interés y una fecha de vencimiento (normalmente 30 años después de su emisión).
Si comprara un bono de $1,000, este pagaría $50 cada año durante 30 años. Al final del año 30, recibiría el pago final de $50, más el capital original de $1,000: un simple pago de intereses del 5% anual.

Interés Simple vs. Interés Compuesto
El interés simple es simplemente eso: simple. El interés compuesto es un poco más complejo a simple vista. Con el interés compuesto, en lugar de simplemente pagar los intereses al final del préstamo, el importe “devuelto” se reinvierte.
Recordemos el ejemplo de nuestro amigo que pidió prestados $100. Cuando llega el momento de pagarnos dentro de un año, justo al entregar los $110, nos pide prestados esos $110 por otro año y paga el mismo interés del 10%. Esto significa que al final del año siguiente, su “pago de intereses” será de $110 * 10% = $11, por lo que el importe total que devolverá será de $121.
Como el amigo pidió prestado el importe total, incluyendo los intereses del primer año, ¡la recompensa es mayor! Esto significa que cada año, el “pago” de cada préstamo se suma al importe original, capitalizando el capital (y los intereses generados) del año siguiente.
Ejemplos de interés compuesto
El interés compuesto se utiliza comúnmente en el ahorro y la inversión. Una cuenta de ahorros es un ejemplo clásico de interés compuesto. Tu banco pagará intereses sobre tus ahorros cada mes, y esos intereses se depositan en la propia cuenta. Esto significa que el mes siguiente generará intereses tanto sobre el depósito original como sobre los intereses generados durante el primer mes.
Invertir en la bolsa también se considera una forma de interés compuesto. Si el valor de una inversión aumenta un 10 % cada año, significa que las ganancias del año anterior se incluyen en las ganancias.
La regla del 72
La Regla del 72 es una forma sencilla de estimar cuánto tardará tu inversión en duplicarse con interés compuesto. Simplemente divide 72 entre la tasa de interés anual (en porcentaje): ¡esto te indica exactamente cuánto tardará la inversión original en duplicarse!
| Tasa de interés | Es hora de duplicar |
|---|---|
| 1% | 72 Years |
| 2% | 36 Years |
| 5% | 14.4 Years |
| 10% | 7.2 Years |
| 20% | 3.6 Years |
Interés compuesto vs. interés simple: En la práctica
Ya hemos visto cómo funcionan el interés simple con un bono y el interés compuesto con una cuenta de ahorros. Pero para comprender por qué el interés compuesto es tan efectivo, analicemos una comparación a 30 años (el vencimiento promedio de un bono) para ver la diferencia de rendimiento entre nuestras dos inversiones.
Interés simple
| Año | Principal | Intereses ganados |
| 1 | $ 1,000 | $50 |
| 2 | $ 1,000 | $50 |
| 3 | $ 1,000 | $50 |
| 4 | $ 1,000 | $50 |
| 5 | $ 1,000 | $50 |
| 6 | $ 1,000 | $50 |
| 7 | $ 1,000 | $50 |
| 8 | $ 1,000 | $50 |
| 9 | $ 1,000 | $50 |
| 10 | $ 1,000 | $50 |
| 11 | $ 1,000 | $50 |
| 12 | $ 1,000 | $50 |
| 13 | $ 1,000 | $50 |
| 14 | $ 1,000 | $50 |
| 15 | $ 1,000 | $50 |
| 16 | $ 1,000 | $50 |
| 17 | $ 1,000 | $50 |
| 18 | $ 1,000 | $50 |
| 19 | $ 1,000 | $50 |
| 20 | $ 1,000 | $50 |
| 21 | $ 1,000 | $50 |
| 22 | $ 1,000 | $50 |
| 23 | $ 1,000 | $50 |
| 24 | $ 1,000 | $50 |
| 25 | $ 1,000 | $50 |
| 26 | $ 1,000 | $50 |
| 27 | $ 1,000 | $50 |
| 28 | $ 1,000 | $50 |
| 29 | $ 1,000 | $50 |
| 30 | $ 1,000 | $50 |
| Total | $1,500 |
Interés compuesto
| Año | Principal | Intereses ganados |
| 1 | $ 1,000 | $ 50 |
| 2 | $ 1,050 | $ 53 |
| 3 | $ 1,103 | $ 55 |
| 4 | $ 1,158 | $ 58 |
| 5 | $ 1,216 | $ 61 |
| 6 | $ 1,276 | $ 64 |
| 7 | $ 1,340 | $ 67 |
| 8 | $ 1,407 | $ 70 |
| 9 | $ 1,477 | $ 74 |
| 10 | $ 1,551 | $ 78 |
| 11 | $ 1,629 | $ 81 |
| 12 | $ 1,710 | $ 86 |
| 13 | $ 1,796 | $ 90 |
| 14 | $ 1,886 | $ 94 |
| 15 | $ 1,980 | $ 99 |
| 16 | $ 2,079 | $ 104 |
| 17 | $ 2,183 | $ 109 |
| 18 | $ 2,292 | $ 115 |
| 19 | $ 2,407 | $ 120 |
| 20 | $ 2,527 | $ 126 |
| 21 | $ 2,653 | $ 133 |
| 22 | $ 2,786 | $ 139 |
| 23 | $ 2,925 | $ 146 |
| 24 | $ 3,072 | $ 154 |
| 25 | $ 3,225 | $ 161 |
| 26 | $ 3,386 | $ 169 |
| 27 | $ 3,556 | $ 178 |
| 28 | $ 3,733 | $ 187 |
| 29 | $ 3,920 | $ 196 |
| 30 | $ 4,116 | $ 206 |
| Total | $3,322 |
En este ejemplo, puedes ver que el interés compuesto ofrece más del doble de rendimiento total que el interés simple. ¡Eso es impresionante! Si observas un gráfico del valor total de tu inversión, también puedes ver una clara diferencia en la forma:
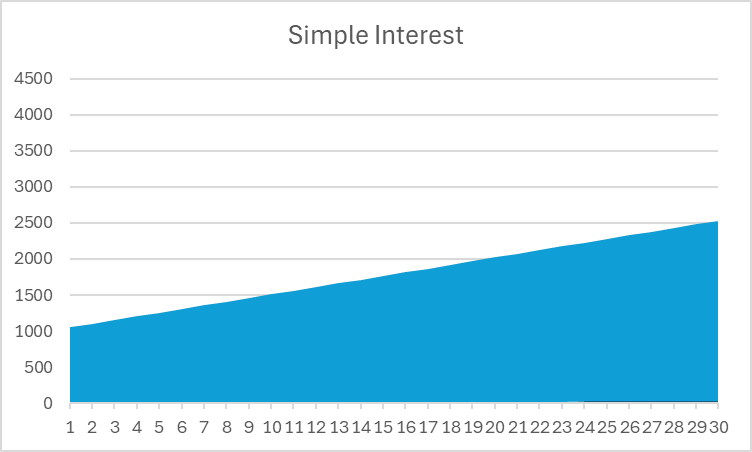
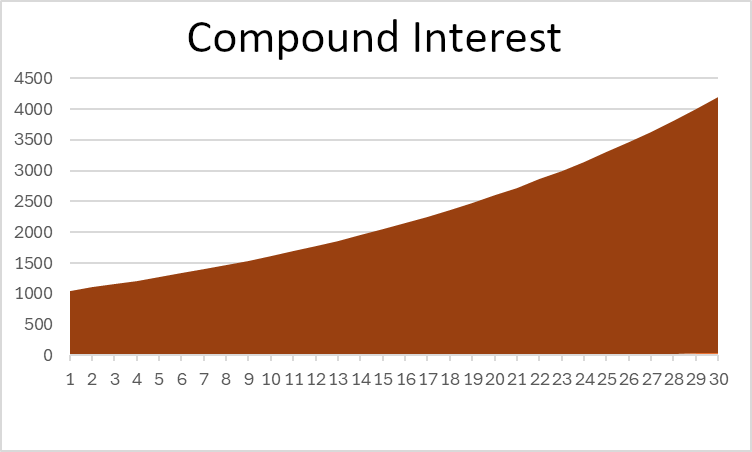
Tenga en cuenta que el interés simple es una línea recta, mientras que el interés compuesto presenta una curva ascendente con el tiempo.
El argumento a favor del interés simple
Aunque definitivamente desea que sus ahorros se capitalicen con el tiempo para obtener una mejor rentabilidad a largo plazo, eso no significa que deba ignorar el interés simple. Simplemente significa que, si desea que sus ahorros se capitalicen, tendrá un poco más de trabajo por delante.
Tomemos como ejemplo la inversión en bonos. Si bien los bonos pagan intereses simples, puede tomar esos pagos y reinvertirlos en otra parte (como depositarlos en una cuenta de ahorros o comprar más bonos), obteniendo así “rendimientos compuestos” a pesar de tener intereses simples.
Siempre que continúe reinvirtiendo sus rendimientos (no gastándolos ni manteniéndolos en efectivo), ¡siempre estará capitalizando!
Frecuencia de capitalización
Hay una última consideración sobre el interés compuesto que puede complicar un poco las cosas: la frecuencia de capitalización.
Mencionamos anteriormente que una cuenta de ahorros paga intereses mensualmente, aunque utiliza una tasa de interés anual del 5%. Esto significa que su banco pagará un interés del 5% / 12 cada mes (o aproximadamente un 0,42%).
Esto significa que su cuenta bancaria se capitaliza a una tasa de interés más baja, pero con mayor frecuencia, que otra cuenta bancaria que solo paga intereses anualmente. Dado que su cuenta se capitaliza con mayor frecuencia, su rendimiento “efectivo” es ligeramente mayor: con una tasa de interés del 5% y $1000 ahorrados, capitalizar una vez generaría $1050, pero capitalizar mensualmente resulta en aproximadamente $1051,16. Esos $1,16 adicionales no son mucho, pero tampoco son insignificantes.

Fórmula de interés compuesto
Gracias al poder de los exponentes, podemos calcular el saldo final de una inversión de interés compuesto sin tener que calcularlo manualmente cada año, como hicimos anteriormente. La fórmula es:
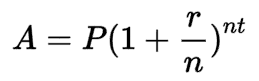
Dónde:
- A es el saldo final
- P es la principal inicial
- r es la tasa de interés (en finanzas, normalmente tasa de interés anual)
- n es el número de períodos en que la inversión se capitaliza
- Y t es el número de períodos de tiempo que estamos midiendo.
En nuestro ejemplo de capitalización anual durante 30 años, P sería $1,000, r sería 5%, n sería 1 (una capitalización al año) y t sería 30, durante 30 años. Si calculáramos el interés mensual, “n” sería 12, ya que se capitaliza 12 veces al año.
Puedes ver la diferencia entre los diferentes tipos de capitalización con diferentes tasas de interés usando nuestra Calculadora de Interés Compuesto.
Return To Glossary