The Magic of Compound Interest
Compound Interest is one of the most important concepts in the modern world, and a cornerstone of the financial system in every economy. The concept of “Compound Interest” is surprisingly simple, but incredibly powerful!
Simple Interest
Before we talk about the power of Compound Interest, we first need to understand Simple Interest.
In the financial world, Simple Interest is the payoff from a loan. For example, if your friend asks to borrow $100 and promises to pay back $110 in return a year from now, you would make a profit of $10 by loaning the money. The “Interest” is the rate of return, or how much profit you made as a percentage of the original investment. In investing terms, the original $100 you invested is called the “Principal”.

Interest = (Pay back – Principal) / Principal
In the example above, the Interest Earned is 10%.
(110 – 100) / 100 = 10%
In the financial world, interest is usually expressed in the return per year. If instead, your friend promised to pay you back in 6 months, then the “annual interest rate” would be adjusted. Since 6 months is ½ of a year, the “annual interest rate” is double the 6 month return.
Annual interest = Interest * Length of the loan, as a percentage of 1 year
So if the friend is paying back in 6 months, the Annual Interest would be 20%.
Annual interest = 10% * 2 = 20%
So given the option between a 20% return (your friend returning the loan, plus $10, in 6 months) instead of a 10% return (friend waiting 12 months to pay back), the 20% return is clearly better.
Simple Interest and Bonds
Bond investing works by simple interest. Bonds typically cost $1,000, and they each have an interest rate and an expiration date (typically 30 years from when it is issued).
If you were to buy a $1,000 bond, this bond will pay out $50 every year, for 30 years. At the end of the 30th year, you will get the final $50 payment, plus your original $1,000 Principal back – a simple 5% interest payment every year.

Simple Interest vs Compound Interest
Simple interest is just that – simple. Compound interest is a bit more complicated on the surface. With compound interest, instead of simply paying out the interest payment at the end of the loan, the “pay back” amount gets re-invested.
Let’s think back to our example of our friend borrowing $100. When he comes to pay us back in 1 year, right as he hands over the $110, he asks to borrow that $110 for another year, and pay the same 10% interest. This means at the end of the next year, his “interest payment” will be $110 * 10% = $11, so the total amount he pays back will be $121.
Because the friend was borrowing the entire amount – including the interest from the first year, the reward is bigger! This means every year, the “payback” from each loan is added onto the original loan amount, “compounding” the principal (and interest earned) in the next year.
Examples of Compound Interest
Compound Interest is commonly used with savings and investing. A savings account is a classic example of compound interest. Your bank will pay interest on your savings every month – and that interest gets deposited into the savings account itself. This means next month, it will earn interest both on the original deposit, plus the interest earned in the first month.
Investing in the stock market is also considered a form of compound interest. If the value of an investment goes up 10% every year, that means the returns of a previous year are included in the gains!
The Rule of 72
The Rule of 72 is a simple way to estimate how long it will take for your investment to double with compound interest. You just divide 72 by the annual interest rate (in percentage form) – this tells you exactly how long it will take for the original investment to double!
| Interest Rate | Time To Double |
|---|---|
| 1% | 72 Years |
| 2% | 36 Years |
| 5% | 14.4 Years |
| 10% | 7.2 Years |
| 20% | 3.6 Years |
Compound vs Simple Interest – In Practice
Now we have seen how simple interest, with a bond, and compound interest, with a savings account, work. But to see why compound interest is so powerful, let’s look at a 30 year comparison (the average expiration length of a bond) to see the difference in return between our two investments.
Simple Interest
| Year | Principal | Interest Earned |
| 1 | $ 1,000 | $50 |
| 2 | $ 1,000 | $50 |
| 3 | $ 1,000 | $50 |
| 4 | $ 1,000 | $50 |
| 5 | $ 1,000 | $50 |
| 6 | $ 1,000 | $50 |
| 7 | $ 1,000 | $50 |
| 8 | $ 1,000 | $50 |
| 9 | $ 1,000 | $50 |
| 10 | $ 1,000 | $50 |
| 11 | $ 1,000 | $50 |
| 12 | $ 1,000 | $50 |
| 13 | $ 1,000 | $50 |
| 14 | $ 1,000 | $50 |
| 15 | $ 1,000 | $50 |
| 16 | $ 1,000 | $50 |
| 17 | $ 1,000 | $50 |
| 18 | $ 1,000 | $50 |
| 19 | $ 1,000 | $50 |
| 20 | $ 1,000 | $50 |
| 21 | $ 1,000 | $50 |
| 22 | $ 1,000 | $50 |
| 23 | $ 1,000 | $50 |
| 24 | $ 1,000 | $50 |
| 25 | $ 1,000 | $50 |
| 26 | $ 1,000 | $50 |
| 27 | $ 1,000 | $50 |
| 28 | $ 1,000 | $50 |
| 29 | $ 1,000 | $50 |
| 30 | $ 1,000 | $50 |
| Total | $1,500 |
Compound Interest
| Year | Principal | Interest Earned |
| 1 | $ 1,000 | $ 50 |
| 2 | $ 1,050 | $ 53 |
| 3 | $ 1,103 | $ 55 |
| 4 | $ 1,158 | $ 58 |
| 5 | $ 1,216 | $ 61 |
| 6 | $ 1,276 | $ 64 |
| 7 | $ 1,340 | $ 67 |
| 8 | $ 1,407 | $ 70 |
| 9 | $ 1,477 | $ 74 |
| 10 | $ 1,551 | $ 78 |
| 11 | $ 1,629 | $ 81 |
| 12 | $ 1,710 | $ 86 |
| 13 | $ 1,796 | $ 90 |
| 14 | $ 1,886 | $ 94 |
| 15 | $ 1,980 | $ 99 |
| 16 | $ 2,079 | $ 104 |
| 17 | $ 2,183 | $ 109 |
| 18 | $ 2,292 | $ 115 |
| 19 | $ 2,407 | $ 120 |
| 20 | $ 2,527 | $ 126 |
| 21 | $ 2,653 | $ 133 |
| 22 | $ 2,786 | $ 139 |
| 23 | $ 2,925 | $ 146 |
| 24 | $ 3,072 | $ 154 |
| 25 | $ 3,225 | $ 161 |
| 26 | $ 3,386 | $ 169 |
| 27 | $ 3,556 | $ 178 |
| 28 | $ 3,733 | $ 187 |
| 29 | $ 3,920 | $ 196 |
| 30 | $ 4,116 | $ 206 |
| Total | $3,322 |
In this example, you can see Compound Interest gives more than double the total return of simple interest – that’s powerful! If you look at a chart of the total value of your investment, you can also see a clear difference in shape:
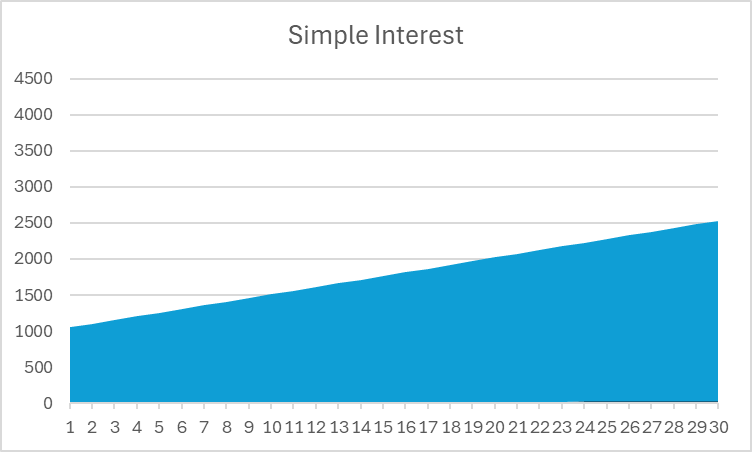
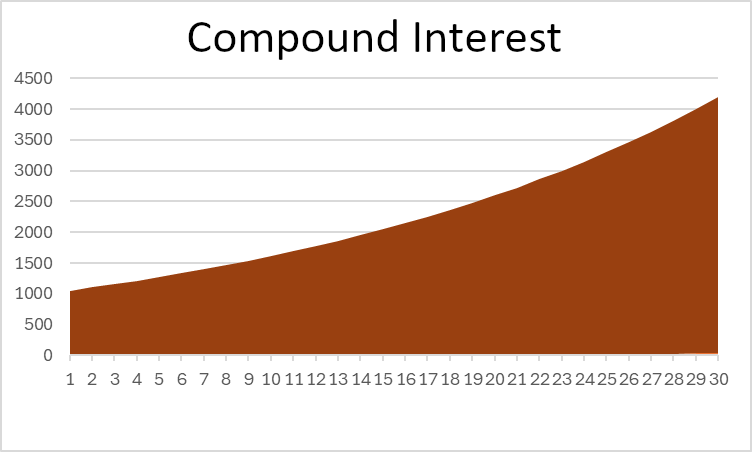
Notice that simple interest is a straight line, while compound interest curves upward over time.
The Case For Simple Interest
Even though you definitely want your savings to compound over time to get a better long-term return, that does not mean simple interest should be ignored. It just means that if you want the savings to compound, you have a bit more work to do.
Take investing in Bonds, for example. While Bonds pay out simple interest, you can take those payments and re-invest them elsewhere (like depositing into a savings account, or buying more bonds) – giving yourself “compounding returns” even though it has simple interest.
So long as you continue to re-invest your returns (not spend it or hold it as cash), you are always compounding!
Compounding Frequency
There is one last consideration with Compound Interest that can make things a bit more complicated – Compounding Frequency.
We mentioned earlier than a savings account pays out interest monthly – even though it uses a 5% annual interest rate. This means that your bank will actually pay out 5% / 12 interest every month (or about 0.42%).
This means that your bank account is compounding at a lower interest rate, but a higher frequency, than a different bank account that only pays its interest annually. Because your account compounds more often, it means your “effective” return is a bit higher – with a 5% interest rate and $1,000 saved, compounding once would yield $1,050, but compounding monthly ends with about $1051.16. That extra $1.16 is not a lot – but it also is not nothing.

Compound Interest Formula
Thanks to the power of Exponents, we can calculate the final balance for a compound interest investment without manually calculating every year, like we did above. The formula is:
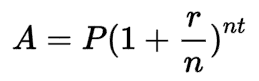
Where:
- A is the final balance
- P is the starting principal
- r is the interest rate (in finance, normally annual interest rate)
- n is the number of periods that the investment compounds
- And t is the number of time periods we are measuring.
In our example of annual compounding for 30 years, P would be $1,000, r would be 5%, n would be 1 (one compound per year), and t would be 30, for 30 years. If we were calculating monthly interest, “n” would instead be 12, since it compounds 12 times per year.
You can see the difference between different types of compounding with different interest rates by playing with our Compound Interest Calculator!
Return To Glossary