Limits and Logs – Personalized Spending and Saving
Much of personal finance is focused on long-term thinking: building your budget so you can save up enough money to live a lifestyle you want, and retire comfortably.
But for each individual person, “a lifestyle you want” and “retire comfortably” can mean very different things. At the end of the day, each person makes a decision every month they work on how much they are going to spend (or consume) and how much they are going to save (or invest).
By understanding the thought process behind this trade-off, you can gain a clearer picture of your own spending. This will help you ensure your actual spending matches your intended spending.
Modelling Consumption – Decreasing Returns to Scale
Much of financial math focuses on exponential growth – how an investment grows based on an interest rate, how a savings account grows over time, or how to build long-term wealth. Exponential functions have an upward curve – investments get bigger over time:

But when you spend instead of save, the benefit you get for each dollar you spend does not have that upward curve. Instead, economists say that consumption has decreasing returns to scale.
Think of it this way – you see two apartments for rent. One has one bedroom, the appliances are 30 years old, the bathroom is tiny, and the kitchen does not even have space for a table. This apartment is listed for $500 / month rent.
The second apartment has brand-new appliances, spacious bathroom with a separate tub and shower, and the kitchen has granite countertops with both space for a table and a breakfast bar. This one is listed for $1,500 / month rent.
Now the second apartment may very well be worth $1,000 more per month. But the value you receive for having an apartment (a place to sleep at night, safely store your belongings, cook and eat food, etc.) is the most important part. If you tried to split out all the different amenities that you get with the more expensive apartment to see where all the value comes from, it might look like this:
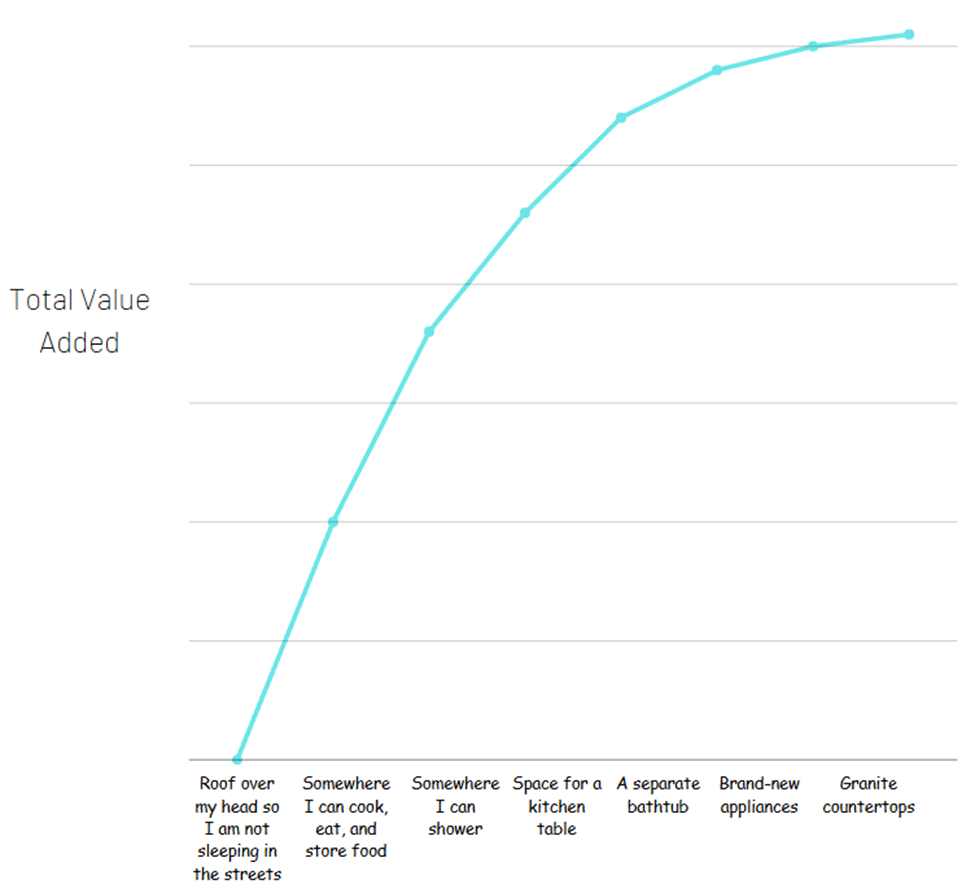
Most of the total value comes from the basics of the basics. That does in no way mean the extras are not worth it – there are no dollar signs here, just how much value you are getting.
In economics, this concept is called utility – the satisfaction or benefit derived from consuming goods or services. You’ll notice that the curve flattens as spending increases. To model this mathematically, we use logarithms instead of exponents.
What is a Logarithm?
You can think of logarithms in relation to exponents the same way that division relates to multiplication – it is the opposite mathematical function. In other words,
If 2^3 = 8, then 3 is the logarithm of 8 to a base of 2.
In economics and finance, logarithms are useful to show these decreasing returns to scale for spending. For example, if we want to make a graph showing the utility received for consumption during a given month, the graph might look like this:
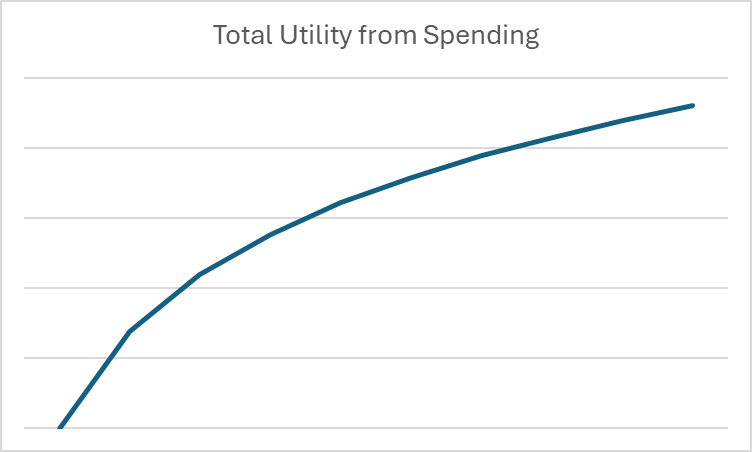
Once we put our spending in the context of logarithms and utility, we can start looking at long-term spending and saving decisions purely in math.
Time Value of Money – Discount Rates
The Time Value of Money refers to the fact that a dollar in the future is worth less than a dollar today. This is because between now and the future, I could have used that dollar to do something – and that opportunity might have passed.
When we want to mathematically describe the Time Value of Money, we use something called a discount rate. The discount rate is a simple number between 0 and 1 that answers this question:
How much would you give up today to get $1 in 1 month?

Every person’s discount rate is different – it refers to how short-term or long-term their personal preferences are. As you might expect, a person with a high discount rate (say, 0.9) is much more likely to be a saver than someone with a low discount rate (say, 0.3). That is because a person with a low discount rate very much values having that money right now – so they are willing to give up 70% of its value to get it immediately instead of waiting.
The discount rate is usually expressed with the Greek letter β. So if your personal discount rate is 0.95, we would say β = 0.95.
Discount Rates and Exponents
Once you can identify your own personal discount rate, you can also use that to figure out how much you would take for that dollar if it is even farther into the future by using exponents.
By raising your beta by an exponent equal to how far in the future we want to calculate, we can say how much that dollar is worth today. In other words, β ^t = how much you would be willing to take today in exchange for a dollar t months from now.
In our example of β = 0.95, this is what a dollar is worth over the next year:
| Months in the Future | How much you would be willing to take today to sacrifice $1 in the future |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
This means that if your β = 0.95, you would be willing to take $0.54 to sacrifice a dollar a year from now.
Now that we have the concept of both logarithms and discount rates, we can put it together to see what it means for long-term saving and spending decisions!
Lifetime Utility
Most of what you learn in a personal finance class is all about saving up for the future, particularly retirement. But that is not really your financial goal in life – you really want to maximize your total lifetime utility. This is why nobody saves every penny – you are balancing your benefit (or utility) from spending today against growing your wealth (through the power of compound interest) so you can spend it in the future.
This means that every month of your life, you have your income for that month, plus all the savings you’ve accumulated until then. These combined resources are what you have to work with. You consciously decide how much of these resources you will spend (or consume) and how much you will save (or invest). You also have some understanding of the interest rate at which your savings will grow over time. In math terms, you are choosing c and i where:
I + (s x (1 + r)) = c + i
Where these variables refer to:
- I = your income this month
- s = how much you already have saved/invested at the start of the month
- r = the interest rate that your savings is growing. So your savings from last month will have grown a little bit by the start of this month than you had last month.
- c = how much you consume/spend this month
- i = how much you save/invest this month
The benefit you are getting from consumption can be expressed by taking the log of your consumption:
Utility = log(c)
You need to determine how much to spend (and consequently save) in each period to maximize your total lifetime utility, not just your happiness in the present moment. Using your discount rate and exponents, we can calculate the utility you will get from consumption in any period in the future, then add them all up.
Total Lifetime Utility =
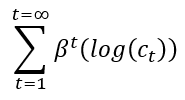
Limits – Utility and Discounts Approaches Zero
At first, it looks like this might be infinite – we are adding up infinite numbers, so it could be getting bigger and bigger forever. However, because t keeps growing, it means the discount applied far in the future starts to get VERY close to zero.
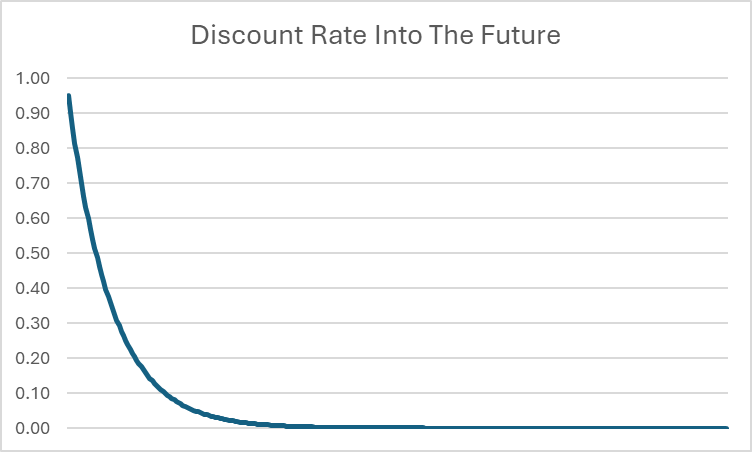
For example, even if β = 0.95, the discount rate in 20 years is all the way down to 0.0000045. The farther in the future it goes, the closer to 0 the discount rate becomes. While the exact maximum amount of lifetime consumption may be impossible to calculate with absolute precision (as it could theoretically involve an infinite number of decimal places), we can confidently state that there exists an upper limit to the total amount of consumption attainable over a lifetime.
Limits are used to define those upward and downward bounds. We can safely say that the discount rate has a lower limit of 0 as t keeps growing to infinity – it will keep approaching 0, but never reach it. The upper limit of total lifetime utility can also be calculated (but doing so does require some advanced calculus, which is not part of this lesson).
Discount Rates and Interest Rates – Choosing To Save
Once we look past all the math, what we can really see is that the decision to spend or save is based really on only two variables:
- Your own personal discount rate (or β)
- The interest rate r, which determines how much your investments will grow
If there are two people who expect the same return on investment for their savings, but we observe one person is a big saver and the other a big spender, we can say that the saver has a higher β than the spender – we can use an actual number to quantify HOW MUCH of a saver or spender someone is.

A strong understanding of interest rates is crucial for financial literacy. If your only savings option is a low-interest savings account (perhaps earning only 3% annually), you’re less likely to prioritize long-term savings goals. This is because you might not fully grasp the potential of higher-risk, higher-reward investments like the stock market.
Ultimately, the most important aspect of financial literacy is being aware of the investment options available to you and making informed decisions based on your individual circumstances and risk tolerance.