Valoración de Activos – Cómo valorar un activo a través de sus finanzas
Cada activo tiene un valor que siempre está cambiando. Entonces, ¿qué factores afectan este cambio? Cosas como anuncios de ganancias, ratios financieros y noticias recientes influyen en el movimiento de la valoración de un activo. La clave de toda valoración de activos es que los ratios y precios son siempre relativos. Esto significa que la mayoría de los métodos de valoración de activos solo pueden comparar una empresa con otra (generalmente en la misma industria) para dar una idea de cuál tiene una ventaja competitiva y está lista para crecer.
Los métodos más comunes de valoración de activos se basan en ratios de los estados financieros de las empresas, y algunas teorías más avanzadas que intentan hacer una valoración más “objetiva”, independientemente de la industria.
Valoración a través de Ratios Financieros
Las dos formas más comunes de dar valor relativo a las empresas es comparando sus ratios de Precio sobre Ganancias y Precio sobre Ventas.
Precio sobre Ganancias (Ratio P/E)
Precio sobre Ganancias = (Precio Actual de la Acción/Ganancias de los últimos 12 meses)
El ratio precio sobre ganancias y el precio sobre ventas son un buen lugar para comenzar. Para el propósito de este artículo, estaremos mirando dos empresas diferentes y sus ratios financieros, Nordstrom (JWN) y Macy’s (M). Calcula este ratio tomando el precio actual de la acción y dividiéndolo por las ganancias por acción de la empresa (obtenidas del Estado de Resultados, que puedes encontrar bajo “Finanzas” en nuestra herramienta de cotizaciones).
| JWN | M | |
| Precio de la Acción | 47.71 | 23.5 |
| Ganancias | 2.02 | 1.99 |
| Ratio P/E | 23.61 | 11.81 |

A partir de este punto, podemos interpretar el valor de una acción usando este ratio para determinar si es una acción de alto crecimiento o defectuosa. Primero echamos un vistazo a Nordstrom y cómo interpretar su ratio P/E. Su ratio P/E actual es 23.61. Luego miramos a Macy’s, con un ratio P/E de 11.81. Los ratios P/E altos se correlacionan con acciones de mayor crecimiento debido a que los inversores encuentran más valor en el precio de las acciones de una empresa. Si esto es cierto, Nordstrom se considera una mejor compra que Macy’s porque los inversores esperan más crecimiento en el futuro.
Precio sobre Ventas
Precio sobre Ventas = (Capitalización de Mercado Actual/Ingresos de los últimos 12 meses)
Un segundo indicador a considerar es el precio sobre ventas, que aunque es similar al precio sobre ganancias, se enfoca en el rendimiento minorista de la empresa. Calcula esto tomando la capitalización de mercado de la empresa y dividiéndola por los ingresos del año. Puedes encontrar la capitalización de mercado actual de una empresa en la página de Cotizaciones estándar, y sus ingresos en su Estado de Resultados (en la sección de Finanzas de la herramienta de cotizaciones, o bajo “Empresa” y “Ratios Clave”).
| 2016 | JWN | M |
| Capitalización de Mercado (En Miles de Millones) | 7.92 | 7.19 |
| Ingresos (En Miles de Millones) | 14.86 | 25.35 |
| Ratio P/S | 0.530 | 0.280 |

Este ratio financiero específico ha sido muy útil durante el último año con respecto a la caída en las tiendas minoristas debido a las compras en línea. Nordstrom tiene un ratio P/S de 0.530 y Macy’s tiene un ratio P/S de 0.280. Esta es una gran herramienta para valorar un activo en comparación con otro en términos de ventas. Este ratio muestra que la capitalización de mercado actual de Nordstrom es mucho más baja de lo que podría ser en términos de sus ingresos en comparación con Macy’s: por cada dólar de valor de la empresa, Macy’s está generando más ventas.
Crecimiento de Ingresos
También es importante observar el crecimiento de los ingresos durante el último año para determinar si este ratio es útil para la valoración. También puedes encontrar esta información en la herramienta de Cotizaciones, bajo la sección “Empresa” y “Ratios Clave”.
| JWN | M | |
| Crecimiento de Ingresos (3 años) | 4.62% | -2.78% |
| Crecimiento de Ingresos (5 años) | 5.47% | -0.99% |
Cuando juntamos los tres, podemos obtener una imagen de qué acción está buscando más crecimiento. Los ratios P/S y P/E son ambos mucho más altos que los de Macy’s, lo que significa que los inversores esperan ver mucho más crecimiento. Esto se respalda con los ingresos de los últimos años, donde Nordstrom ha estado creciendo mucho más rápido, dando más valor a sus accionistas.
Teorías y Modelos:
Los ratios financieros en sí son un gran indicador del rendimiento futuro de un activo, sin embargo, hay teorías y modelos que se utilizan para determinar cosas como el retorno esperado. Los más pertinentes son la teoría de precios de arbitraje y el modelo de precios de activos de capital, o CAPM para abreviar. Ambas fórmulas utilizan variables similares, por lo que es importante identificarlas primero:
Tasa libre de riesgo (rf)
El retorno esperado en un activo sin riesgo, como un Bono del Tesoro de EE. UU. Esto se debe a que el Tesoro de EE. UU. nunca incumplirá.
Riesgo en el Mercado (rm)
Este es un riesgo amplio, que incluye los riesgos enfrentados por los mercados financieros, pero algunos de ellos incluyen recesiones, agitación política, cambios en las tasas de interés, etc. Hay muchas formas diferentes de calcular esto a partir de diferentes fuentes.
Prima de Riesgo del Mercado (rm – rf) = rp
Esto es simplemente el riesgo en el mercado menos la tasa libre de riesgo. Cuánto puede ganar un inversor al invertir en un activo más arriesgado.
Beta (β)
La medida del riesgo de un activo. Puedes obtener esto de la página de Cotizaciones para casi cualquier acción.
Sensibilidad de un activo a un factor (b)
Así es como el precio de un activo se ve afectado por el movimiento de otro activo. Esta sensibilidad puede ser cualquier cosa, básicamente cualquier variable que desees incluir en tu modelo que creas que impactará el precio de la acción.
Teoría de Precios de Arbitraje (APT)
Comenzaremos con la teoría de precios de arbitraje, la fórmula es la siguiente:
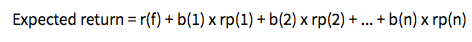

Para usar este modelo, comienza tomando la tasa de retorno libre de riesgo, luego añade cómo crees que muchas variables diferentes impactarán el precio. Cada “b” en la fórmula es otro factor que crees que tendrá un impacto, y puedes tener tantos factores como desees. Podrías basar la fórmula en la tasa de inflación, tasas de cambio, tasas de producción, etc. Las posibilidades son infinitas.
La valoración que obtienes de esta fórmula se considera el retorno esperado de un activo. Supongamos que intentas encontrar el retorno esperado de Tesla (TSLA). Algunas variables diferentes que podrías usar serían los precios del petróleo, los precios de la electricidad y las tasas de préstamos para automóviles. Estas tres tienen una correlación directa con el rendimiento de las ventas de Tesla durante el próximo año y, por lo tanto, su precio de acción. Si las tasas de préstamos para automóviles aumentan, puedes esperar que el retorno esperado de Tesla disminuya. Si los precios del petróleo aumentan, puedes esperar que su retorno esperado aumente debido a que más personas cambian a vehículos eléctricos. Es una gran herramienta para incluir variables que de otro modo se ignorarían.
Usando la Teoría de Precios de Arbitraje
Para poner esta fórmula en acción, primero identifica varios factores que deberían impactar el precio de la acción, que serían los factores “b”. Por ejemplo, con Tesla, podríamos decir:
- b(1) = Crecimiento en el precio del petróleo
- b(2) = Crecimiento en el precio de la electricidad
- b(3) = Crecimiento en las tasas de interés de préstamos para automóviles
A continuación, piensa en cómo cada uno de estos factores influye en el precio de la acción (rp, o “Prima de Riesgo”). Puedes usar Regresión Lineal para calcular estas variables en Excel o cualquier otro programa de hojas de cálculo, los valores a continuación son solo un ejemplo.
- rp(1) = 0.7, lo que significa que esperamos que un aumento del 1% en el precio del petróleo haga que el precio de la acción de Tesla suba un 4%
- rp(2) = -0.5, lo que significa que esperamos que un aumento del 1% en el precio de la electricidad haga que el precio de la acción de Tesla baje un 0.5%
- rp(3) = -2, lo que significa que esperamos que un aumento del 1% en las tasas de interés de préstamos para automóviles haga que el precio de la acción de Tesla baje un 2%
A continuación, solo necesitamos obtener los valores reales de cómo esperamos que se muevan todas estas tasas en el próximo año, luego introducir estos números en la fórmula.
- Se espera que los precios del petróleo bajen en 2017 alrededor del 4%
- Se espera que los precios de la electricidad bajen en 2017 alrededor del 2%
- Se espera que las tasas de interés de préstamos para automóviles bajen un 3%
- La tasa libre de riesgo actual (valorada por un bono del tesoro a 10 años) es del 2.35%
Finalmente, introduce estos valores en la fórmula:
Tasa de Retorno Esperada = (rf) + b(1) * rp(1) + b(2) * rp(2) + b(3) * rp(3)
= 2.35% + (-4% * 0.7) + (-2% * 0.5) + (-3% * -2)
= 2.35% – 2.8% + 1% + 6%
= 6.55%
Entonces, una acción tiene este retorno esperado dado la sensibilidad hacia estos factores del 6.55%
Modelo de Valoración de Activos de Capital (CAPM)
El modelo de valoración de activos de capital es la siguiente fórmula:
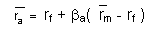
En términos simples, esta fórmula significa que la tasa de retorno promedio esperada se basa en la tasa libre de riesgo, más el Beta de nuestra acción, modificado por el riesgo promedio en el mercado en general.
Para esto simplemente introducimos las variables anteriores, recordando el orden de las operaciones y recibirás un retorno esperado sobre un activo. Lo grandioso de esta fórmula es que es bastante simple y toda la información necesaria está listada públicamente y es fácil de acceder. Es importante tener en cuenta que, aunque esto te da un retorno esperado, no es el número más preciso y siempre se debe investigar más sobre un activo antes de invertir. Ahora veremos un ejemplo de CAPM usando la acción de Nordstrom como ejemplo. JWN actualmente tiene un beta de 0.71111, y usaremos 4.04% como nuestra tasa de Riesgo en el Mercado (derivada aquí).
Retorno Esperado = 2.35% + 0.71111(4.04%-2.35%)
= 2.35% + 0.7111 * 1.69%
= 2.35% + 1.201%
Retorno Esperado = 3.5517%