Évaluation d’actifs – Comment évaluer un actif grâce à ses données financières
Chaque actif a une valeur en constante évolution. Quels facteurs influencent cette évolution ? Les annonces de résultats, les ratios financiers et l’actualité récente influencent tous la valorisation d’un actif. L’essentiel de toute évaluation d’actifs est que les ratios et les prix sont toujours relatifs. Cela signifie que la plupart des méthodes d’évaluation d’actifs ne peuvent que comparer une entreprise à une autre (généralement du même secteur) pour déterminer laquelle présente un avantage concurrentiel et est prête à croître.
Les méthodes d’évaluation d’actifs les plus courantes s’appuient sur les ratios des états financiers des entreprises et sur des théories plus avancées qui tentent d’établir une évaluation plus objective, quel que soit le secteur.
Évaluation par ratios financiers
Les deux manières les plus courantes d’attribuer une valeur relative aux entreprises consistent à comparer leurs ratios cours/bénéfice et cours/ventes.
Ratio cours/bénéfice (PE)
Prix sur bénéfices = (Prix actuel de l’action/Bénéfices des 12 derniers mois)
Le ratio cours/bénéfice et le ratio cours/chiffre d’affaires constituent un bon point de départ. Dans cet article, nous examinerons deux entreprises différentes et leurs ratios financiers : Nordstrom (JWN) et Macy’s (M). Calculez ce ratio en divisant le cours actuel de l’action par le bénéfice par action de l’entreprise (obtenu à partir du compte de résultat, disponible sous « Finances » dans notre outil de cotation).
| JWN | M | |
| Cours de l’action | 47.71 | 23.5 |
| Gains | 2.02 | 1.99 |
| Ratio cours/bénéfice | 23.61 | 11.81 |

À partir de ce point, nous pouvons interpréter la valeur d’une action en utilisant ce ratio pour déterminer s’il s’agit d’une action à forte croissance ou d’une action imparfaite. Nous examinons d’abord Nordstrom et comment interpréter son ratio cours-bénéfice. Leur ratio cours-bénéfice actuel est de 23,61. Nous examinons ensuite Macy’s, avec un ratio cours-bénéfice de 11,81. Des ratios cours-bénéfice élevés sont corrélés à des actions à plus forte croissance, car les investisseurs trouvent plus de valeur dans le cours de l’action d’une entreprise. Si cela se vérifie, Nordstrom est considéré comme un meilleur achat que Macy’s, car les investisseurs s’attendent à une croissance plus importante à l’avenir.
Prix par rapport aux ventes
Prix sur ventes = (capitalisation boursière actuelle/chiffre d’affaires au cours des 12 derniers mois)
Un deuxième indicateur à considérer est le ratio cours/ventes. Bien que similaire au ratio cours/bénéfice, il reflète la performance commerciale de l’entreprise. Pour le calculer, divisez la capitalisation boursière de l’entreprise par son chiffre d’affaires annuel. La capitalisation boursière actuelle d’une entreprise est disponible sur la page « Cours » standard, et son chiffre d’affaires dans son compte de résultat (dans la section « Finances » de l’outil de cotation, ou sous « Entreprise » et « Ratios clés »).
| 2016 | JWN | M |
| Capitalisation boursière (en milliards) | 7.92 | 7.19 |
| Chiffre d’affaires (en milliards) | 14.86 | 25.35 |
| Rapport P/S | 0.530 | 0.280 |

Ce ratio financier spécifique s’est avéré très utile l’année dernière face à la chute des ventes en ligne dans le commerce de détail. Nordstrom affiche un ratio cours/valeur de 0,530 et Macy’s un ratio cours/valeur de 0,280. C’est un excellent outil pour évaluer un actif par rapport à un autre en termes de chiffre d’affaires. Ce ratio montre que la capitalisation boursière actuelle de Nordstrom est bien inférieure à ce qu’elle pourrait être en termes de chiffre d’affaires par rapport à celle de Macy’s : par dollar investi, Macy’s réalise davantage de ventes.
Growth of Revenue
Il est également important d’examiner la croissance du chiffre d’affaires au cours de l’année écoulée afin de déterminer si ce ratio est utile à la valorisation. Vous trouverez également ces informations dans l’outil « Devis », sous la section « Entreprise » et « Ratios clés ».
| JWN | M | |
| Croissance des revenus (3 ans) | 4.62% | -2.78% |
| Croissance des revenus (5 ans) | 5.47% | -0.99% |
En combinant ces trois éléments, nous pouvons déterminer quelle action vise la plus forte croissance. Les ratios cours/bénéfice et cours/bénéfice sont tous deux bien supérieurs à ceux de Macy’s, ce qui signifie que les investisseurs anticipent une croissance nettement supérieure. Ceci est confirmé par le chiffre d’affaires de Nordstrom ces dernières années, qui a connu une croissance beaucoup plus rapide, offrant ainsi plus de valeur à ses actionnaires.
Théories et modèles :
Les ratios financiers sont en eux-mêmes un excellent indicateur de la performance future d’un actif. Cependant, il existe des théories et des modèles permettant de déterminer des éléments tels que le rendement attendu. Les plus pertinents sont la théorie de l’arbitrage des prix et le modèle d’évaluation des actifs financiers (MEDAF). Ces deux formules utilisent des variables similaires ; il est donc important de les identifier au préalable :
Taux sans risque (tsr)
Rendement attendu d’un actif sans risque, tel qu’un bon du Trésor américain. Ce taux s’explique par le fait que le Trésor américain ne fera jamais défaut.
Risque de marché (rm)
Il s’agit d’un risque général qui inclut les risques auxquels sont confrontés les marchés financiers, notamment les récessions, les turbulences politiques, les variations de taux d’intérêt, etc. Il existe de nombreuses façons de le calculer à partir de différentes sources.
Prime de risque de marché (rm – rf) = rp
Il s’agit simplement du risque de marché soustrait du taux sans risque. Il s’agit du gain qu’un investisseur peut tirer d’un investissement dans un actif plus risqué.
Bêta (β)
Mesure du risque d’un actif. Vous pouvez l’obtenir sur la page Cotations de presque toutes les actions.
Sensibilité d’un actif à un facteur (b)
Il s’agit de l’impact du cours d’un actif sur la variation d’un autre actif. Cette sensibilité peut être n’importe quelle variable que vous souhaitez inclure dans votre modèle et qui, selon vous, aura un impact sur le cours de l’action.
Théorie des prix d’arbitrage (APT)
Nous commencerons par la théorie des prix d’arbitrage, la formule est la suivante :
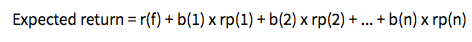

Pour utiliser ce modèle, commencez par prendre le taux de rendement sans risque, puis ajoutez-y l’impact que vous pensez avoir sur le prix. Chaque « b » de la formule représente un facteur qui, selon vous, aura un impact, et vous pouvez en inclure autant que vous le souhaitez. Vous pouvez baser la formule sur le taux d’inflation, les taux de change, les taux de production, etc. Les possibilités sont infinies.
La valorisation obtenue à partir de cette formule est considérée comme le rendement attendu d’un actif. Imaginons que vous cherchiez à déterminer le rendement attendu de Tesla (TSLA). Parmi les variables à prendre en compte, on peut citer le prix du pétrole, le prix de l’électricité et les taux de crédit automobile. Ces trois variables sont directement liées aux ventes de Tesla l’année prochaine et, par conséquent, au cours de son action. Si les taux de crédit automobile augmentent, le rendement attendu de Tesla devrait baisser. Si le prix du pétrole augmente, son rendement attendu devrait augmenter en raison de l’augmentation du nombre de personnes passant aux véhicules électriques. C’est un excellent outil pour intégrer des variables qui seraient autrement négligées.
Utilisation de la théorie de l’arbitrage des prix
Pour mettre cette formule en pratique, il faut d’abord identifier plusieurs facteurs susceptibles d’influencer le cours de l’action, appelés facteurs « b ». Par exemple, pour Tesla, on pourrait dire :
- b(1) = Croissance du prix du pétrole
- b(2) = Croissance du prix de l’électricité
- b(3) = Croissance des taux d’intérêt des prêts automobiles
Ensuite, réfléchissez à l’influence de chacun de ces facteurs sur le cours de l’action (prime de risque). Vous pouvez utiliser la régression linéaire pour calculer ces variables dans Excel ou tout autre tableur. Les valeurs ci-dessous ne sont qu’un exemple.
- rp(1) = 0,7 : une hausse de 1 % du prix du pétrole devrait entraîner une hausse de 4 % du cours de l’action Tesla.
- rp(2) = -0,5 : une hausse de 1 % du prix de l’électricité devrait entraîner une baisse de 0,5 % du cours de l’action Tesla.
- rp(3) = -2 : une hausse de 1 % des taux d’intérêt des prêts automobiles devrait entraîner une baisse de 2 % du cours de l’action Tesla.
Ensuite, nous devons simplement obtenir les valeurs réelles de la façon dont nous prévoyons que tous ces taux évolueront au cours de l’année prochaine, puis insérer ces chiffres dans la formule.
- Les prix du pétrole devraient baisser d’environ 4 % en 2017.
- Les prix de l’électricité devraient baisser d’environ 2 % en 2017.
- Les taux d’intérêt des prêts automobiles devraient baisser de 3 %.
- Le taux sans risque actuel (évalué par un bon du Trésor à 10 ans) est de 2,35 %.
Enfin, insérez ces valeurs dans la formule :
Expected Rate of Return = (rf) + b(1) * rp(1) + b(2) * rp(2) + b(3) * rp(3)
= 2.35% + (-4% * 0.7) + (-2% * 0.5) + (-3% * -2)
= 2.35% – 2.8% + 1% + 6%
= 6.55%
So, a stock has this expected return given sensitivity towards these factors of 6.55%
Ainsi, une action a ce rendement attendu compte tenu de la sensibilité à ces facteurs de 6,55 %
Le modèle d’évaluation des actifs financiers est la formule suivante :
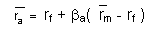
En termes simples, cette formule signifie que le taux de rendement moyen attendu est basé sur le taux sans risque, plus le bêta de notre action, modifié par le risque moyen sur le marché global.
Pour cela, il suffit d’insérer les variables ci-dessus, en respectant l’ordre des opérations, et vous obtiendrez le rendement attendu d’un actif. L’avantage de cette formule est sa simplicité : toutes les informations nécessaires sont publiques et facilement accessibles. Il est important de garder à l’esprit que, même si cela donne un rendement attendu, ce n’est pas le chiffre le plus précis ; il est donc conseillé de toujours se renseigner davantage sur un actif avant d’investir. Nous allons maintenant examiner un exemple de CAPM en prenant l’action Nordstrom comme exemple. JWN a actuellement un bêta de 0,71111, et nous utiliserons 4,04 % comme taux de risque de marché (dérivé ici).
Expected Return = 2.35% + 0.71111(4.04%-2.35%)
= 2.35% + 0.7111 * 1.69%
= 2.35% + 1.201%
Expected Return = 3.5517%