Spese Discrezionali – Comprendere la Tendenza Centrale
Cosa Sono le Spese Discrezionali?
Le spese discrezionali sono acquisti non essenziali— desideri, cose che compriamo per piacere, comodità o divertimento. Esempi includono intrattenimento, cene fuori o gli ultimi gadget tecnologici. Al contrario, necessità sono essenziali per la sopravvivenza: cibo, alloggio, utenze e assistenza sanitaria. Conoscere la differenza tra necessità e desideri è una competenza finanziaria chiave, soprattutto quando inizi a gestire il tuo denaro.

Perché È Importante
Comprendere la differenza tra necessità e desideri ti aiuta a fare scelte finanziarie più intelligenti. Ad esempio, se hai risparmiato per un nuovo videogioco ma il tuo telefono si rompe, cosa scegli? Il telefono è una necessità; il gioco è un desiderio. Scegliere di sostituire il telefono assicura che tu soddisfi una spesa necessaria, preparandoti per la sicurezza finanziaria a lungo termine.
Analizzare Necessità vs. Desideri: Un Approccio Dati
Monitorare le tue spese aiuta a rivelare schemi nelle tue abitudini finanziarie. Potresti tenere traccia di quanto spendi tu e i tuoi amici per articoli non essenziali come snack, intrattenimento o app. Esaminando questi dati, puoi riflettere se le tue spese sono in linea con le tue priorità.
Infatti, le ricerche mostrano che le persone che pensano a lungo termine tendono a risparmiare di più, mentre quelle concentrate sulla gratificazione immediata sono più propense a spendere eccessivamente. Analizzare i tuoi dati di spesa può aiutarti a prendere decisioni finanziarie migliori e a costruire abitudini di spesa più sane.
Utilizzare la Tendenza Centrale per Analizzare i Dati di Spesa
Quando analizzi le spese, tre misure chiave di tendenza centrale—media, mediana e moda—aiutano a riassumere il tuo comportamento finanziario:
- Media: La media di tutte le tue spese. Sebbene utile, la media può essere distorta da valori estremi (come qualcuno che spende molto di più o di meno rispetto agli altri).
- Mediana: Il valore centrale quando tutti i dati sono ordinati. Questo fornisce un’idea migliore delle spese tipiche evitando i valori anomali.
- Moda: Il valore più frequente. Questo può aiutare a identificare abitudini comuni o tendenze popolari nelle spese.
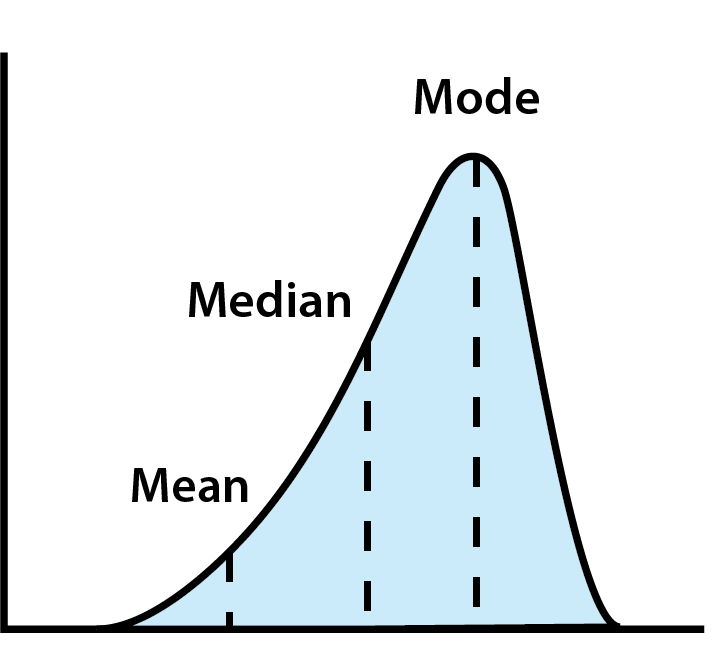
Utilizzare la Tendenza Centrale per Analizzare i Dati di Spesa
Guardare la tendenza centrale può aiutare a mettere in prospettiva il tuo budget. Ad esempio, potresti comprare un caffè ogni mattina mentre vai a scuola o al lavoro. Ti rendi conto che questo può accumularsi, ma pensi di spendere più o meno quanto la persona accanto a te, quindi è una spesa ragionevole.
Ma se chiedi effettivamente a un gruppo di tuoi coetanei quanto spendono, può darti una visione più ampia di quanto stai realmente spendendo ogni mese.
- Media: Se scopri che stai spendendo più o meno quanto la media, allora avevi ragione riguardo alle tue abitudini di spesa. Ma se scopri che stai spendendo molto di più rispetto agli altri, potresti dare un’occhiata più da vicino alle tue scelte di bevande.
- Mediana: La mediana ti dice come le tue azioni si inseriscono rispetto a tutti gli altri. Forse diverse persone spendono $0 per il caffè – questo farebbe abbassare la media rispetto a quanto spende un tipico bevitore di caffè. In questo caso, potresti vedere che in realtà spendi meno della mediana, quindi le tue spese sono effettivamente ragionevoli.
- Moda: Il valore più frequente. Forse un gruppo di amici ordina lo stesso Orange Mocha Frappuccino ogni mattina – rendendolo la scelta moda. Se sai che l’Orange Mocha Frappuccino è costoso, potrebbe significare che la mediana è anche distorta verso l’alto rispetto a quanto pensi che un tipico bevitore di caffè ordini.
Esempio: L’Abitudine al Caffè di Esteban
Esteban compra un caffè da $4.75 ogni mattina. Sebbene creda che questo sia un prezzo ragionevole, è curioso di sapere se è tipico. Per avere un’idea migliore del costo medio, chiede ai suoi amici, familiari e colleghi quanto hanno speso per il loro caffè mattutino. Queste sono le loro risposte:

| Rispondente | Quanto Hanno Speso Questa Mattina |
|---|---|
| 1 | $0.00 |
| 2 | $6.95 |
| 3 | $1.99 |
| 4 | $0.00 |
| 5 | $4.25 |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. Calcolare la Media
Per prima cosa, Esteban vuole testare la sua prima ipotesi – che sta spendendo circa la media di tutti gli altri. Quindi, calcolerebbe la media, o media aritmetica. La formula per calcolare la media è:
Media = somma delle osservazioni / numero delle osservazioni
La formula può essere scritta anche in quella che viene chiamata Notazione Sigma:
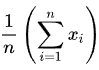
Con la Notazione Sigma, il segno Sigma (Σ) significa “somma”, il segno n significa quante osservazioni, il x significa per una specifica osservazione, e il i significa per ogni osservazione. Quindi ciò che questo sta dicendo è che dalla prima (i = 1, in fondo alla sigma) all’ultima osservazione (fino a n, che è in cima alla sigma), somma tutti i loro valori, poi moltiplica per 1/n. La Notazione Sigma è molto comune nei campi di ricerca, poiché mostra operazioni algebriche o matematiche applicate a un’intera serie di numeri, invece che uno alla volta.
Quindi sommiamo tutte le osservazioni:
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
E dividiamo per 15 (numero delle osservazioni)
$78.10 / 15 = $5.21
Esteban aveva ragione – sta spendendo meno della media. I suoi $4.75 sono più economici del valore medio di $5.21.
2. Calcolare la Mediana
Per calcolare la mediana, dobbiamo riordinare gli ordini dal più piccolo al più grande. La mediana è il numero centrale.
| Rispondente | Quanto hanno speso questa mattina |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
Il valore centrale (mediana) delle spese per il caffè mattutino dei suoi amici, familiari e colleghi è in realtà $3.00, significativamente inferiore ai $4.75 di Esteban. Questa scoperta fa sentire Esteban meno a suo agio riguardo alla sua abitudine quotidiana al caffè. Si rende conto di spendere il 50% in più rispetto ai suoi coetanei, anche se il suo costo individuale è al di sotto del prezzo medio.
3. Calcolare la Moda
Infine, Esteban vuole vedere qual è la scelta più popolare. Per questo, deve trovare la moda. La moda è semplicemente l’osservazione più comune. Nel caso del suo sondaggio, 5 persone hanno risposto $0.00 – rendendo questa la scelta più comune (la moda). Anche se non è la maggioranza delle persone, questo ha sicuramente un grande impatto sulle scelte di media e mediana. Esteban non è del tutto sicuro di cosa fare con queste informazioni – ma ci sono ulteriori calcoli per aiutarlo a trovare una risposta!
Interpretare i Dati: Asimmetria, Outlier e Distribuzioni
Esteban sta esaminando i problemi nella sua analisi derivanti dalla distribuzione delle sue risposte – o come le sue risposte appaiono su un grafico.
Asimmetria
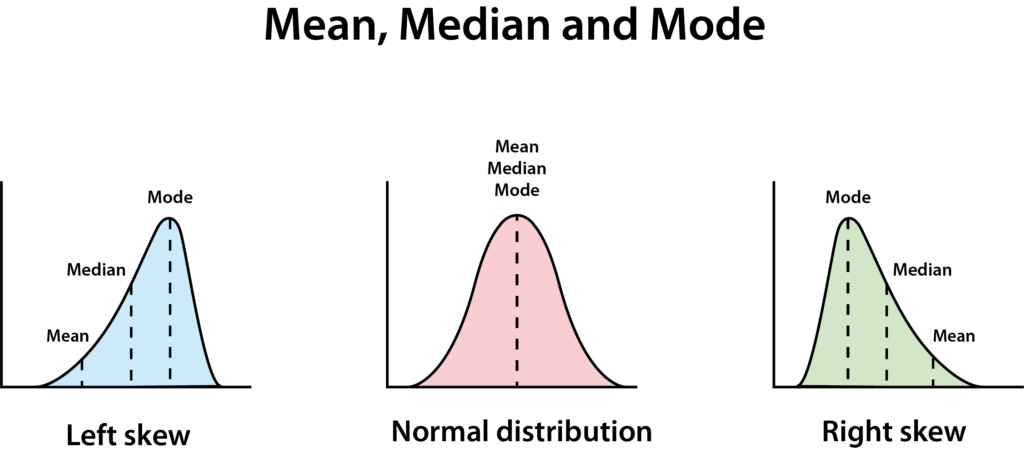
Una distribuzione normale ha una forma a campana pulita. Una distribuzione perfettamente normale porta a media, mediana e moda tutte uguali.
Se non sono tutte uguali, significa che i dati sono asimmetrici – in questo caso, diciamo che i suoi dati hanno una distribuzione asimmetrica a destra, il che significa che la mediana è inferiore alla media. Questo accade spesso quando ci sono pochi numeri davvero grandi o davvero piccoli, facendo sembrare il grafico avere una lunga discesa verso destra.
Valori anomali
Quando Esteban esamina attentamente le risposte, nota un valore anomalo: un costo di $24.68. Questo valore è significativamente più alto di qualsiasi altro. I valori anomali sono punti dati che sono molto distanti dal resto del gruppo e vengono spesso esclusi dall’analisi statistica perché possono distorcere i risultati.
In seguito a ulteriori indagini, Esteban scopre che questo valore anomalo rappresenta il costo di un gallone di succo d’arancia appena spremuto acquistato per l’intera famiglia di quella persona quella mattina. Questa spesa non è chiaramente comparabile al costo tipico di una singola tazza di caffè.
Distribuzioni bimodali
Le distribuzioni bimodali si verificano quando si guarda la distribuzione di frequenza e non si vede solo un picco, ma due (o più). Dai un’occhiata a queste risposte del sondaggio su quanto hanno pagato gli studenti delle scuole superiori per i loro pranzi in un determinato giorno:
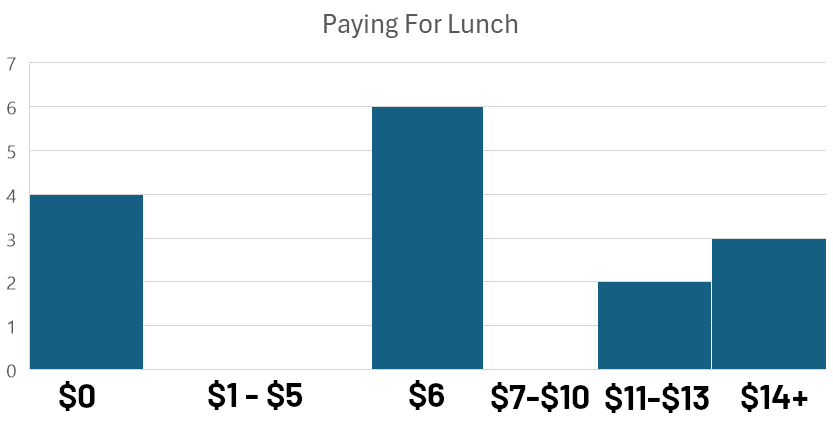
Questo tipo di grafico, in cui i dati sono raggruppati in intervalli o ‘bin’ per un confronto visivo, è chiamato istogramma. L’analisi di come le osservazioni sono distribuite all’interno di questi bin è nota come analisi di frequenza.
Osservando l’istogramma, notiamo due picchi distinti: uno vicino a $0 e un altro vicino a $6. Questa distribuzione bimodale (con modalità vicino a $0 e $6) suggerisce che ci sono due gruppi distinti all’interno dei dati.
Identificare questi picchi può guidare ulteriori ricerche ponendo domande come:
- Quali fattori potrebbero spiegare questi due distinti modelli di spesa?
- Cosa rivelano questi picchi sulle motivazioni e i comportamenti sottostanti degli individui in questi gruppi?
Inoltre, la presenza di questi due picchi indica una distribuzione asimmetrica a destra, il che significa che una maggiore proporzione dei punti dati è raggruppata verso l’estremità inferiore della gamma di prezzi.
I dati bimodali non significano necessariamente che ci siano due risposte con lo stesso numero esatto di osservazioni, solo che possiamo vedere due picchi chiari (in questo caso $6 è la “Vera Moda”).
Quando i ricercatori hanno esaminato più da vicino i dati, la spiegazione è diventata ovvia. $0 erano studenti che portavano un pranzo da casa e $6 era il costo del pranzo scolastico regolare. Gli studenti che pagavano più di $10 stavano acquistando una combinazione di articoli dal bar della scuola e altri cibi che avevano comprato lungo la strada per la scuola.

Conclusione: Usare i dati per prendere decisioni finanziarie migliori
Comprendendo queste tre misure di tendenza centrale: media, mediana e moda, puoi interpretare i dati e prendere decisioni finanziarie più informate. Che tu stia analizzando le tue spese o guardando tendenze più ampie, questi strumenti ti permettono di sviluppare migliori abitudini di spesa. Raccogliere e analizzare i dati di spesa può fornire informazioni sul tuo comportamento finanziario.
Per studenti come Esteban, cambiamenti semplici—come ridurre le spese discrezionali—possono portare a benefici finanziari a lungo termine. Quando Esteban vede che le sue spese sono superiori alla mediana – e che la scelta più popolare è non spendere affatto, questo aiuta a contestualizzare le sue decisioni di spesa e cosa ciò significa per il suo futuro.