Όρια και Καταγραφές – Προσωποποιημένες Δαπάνες και Αποταμιεύσεις
Πολλές πτυχές των προσωπικών οικονομικών επικεντρώνονται στη μακροχρόνια σκέψη: να χτίσετε τον προϋπολογισμό σας ώστε να μπορέσετε να αποταμιεύσετε αρκετά χρήματα για να ζήσετε τον τρόπο ζωής που θέλετε και να συνταξιοδοτηθείτε άνετα.
Αλλά για κάθε άτομο, “ένας τρόπος ζωής που θέλετε” και “να συνταξιοδοτηθείτε άνετα” μπορεί να σημαίνει πολύ διαφορετικά πράγματα. Στο τέλος της ημέρας, κάθε άτομο παίρνει μια απόφαση κάθε μήνα σχετικά με το πόσα θα ξοδέψει (ή θα καταναλώσει) και πόσα θα αποταμιεύσει (ή θα επενδύσει).
Κατανοώντας τη διαδικασία σκέψης πίσω από αυτή την ανταλλαγή, μπορείτε να αποκτήσετε μια πιο καθαρή εικόνα των δικών σας δαπανών. Αυτό θα σας βοηθήσει να διασφαλίσετε ότι οι πραγματικές σας δαπάνες ταιριάζουν με τις προγραμματισμένες σας δαπάνες.
Μοντελοποίηση Κατανάλωσης – Μειούμενες Αποδόσεις Κλίμακας
Πολλές πτυχές των χρηματοοικονομικών μαθηματικών επικεντρώνονται στην εκθετική ανάπτυξη – πώς μια επένδυση αυξάνεται με βάση ένα επιτόκιο, πώς ένας λογαριασμός αποταμίευσης αυξάνεται με την πάροδο του χρόνου ή πώς να χτίσετε μακροχρόνιο πλούτο. Οι εκθετικές συναρτήσεις έχουν μια ανοδική καμπύλη – οι επενδύσεις γίνονται μεγαλύτερες με την πάροδο του χρόνου:

Αλλά όταν ξοδεύετε αντί να αποταμιεύετε, το όφελος που αποκτάτε για κάθε δολάριο που ξοδεύετε δεν έχει αυτή την ανοδική καμπύλη. Αντίθετα, οι οικονομολόγοι λένε ότι η κατανάλωση έχει μειούμενες αποδόσεις κλίμακας.
Σκεφτείτε το έτσι – βλέπετε δύο διαμερίσματα προς ενοικίαση. Το ένα έχει ένα υπνοδωμάτιο, οι συσκευές είναι 30 ετών, το μπάνιο είναι μικροσκοπικό και η κουζίνα δεν έχει καν χώρο για τραπέζι. Αυτό το διαμέρισμα είναι καταχωρημένο για $500 / μήνα ενοίκιο.
Το δεύτερο διαμέρισμα έχει ολοκαίνουργιες συσκευές, ευρύχωρο μπάνιο με ξεχωριστή μπανιέρα και ντους, και η κουζίνα έχει γρανίτες με χώρο για τραπέζι και μπαρ πρωινού. Αυτό είναι καταχωρημένο για $1,500 / μήνα ενοίκιο.
Τώρα το δεύτερο διαμέρισμα μπορεί πολύ καλά να αξίζει $1,000 περισσότερα το μήνα. Αλλά η αξία που λαμβάνετε για το να έχετε ένα διαμέρισμα (ένας χώρος για να κοιμάστε τη νύχτα, να αποθηκεύετε με ασφάλεια τα πράγματά σας, να μαγειρεύετε και να τρώτε φαγητό, κ.λπ.) είναι το πιο σημαντικό μέρος. Αν προσπαθήσετε να διαχωρίσετε όλες τις διαφορετικές ανέσεις που έχετε με το πιο ακριβό διαμέρισμα για να δείτε από πού προέρχεται όλη η αξία, μπορεί να φαίνεται έτσι:
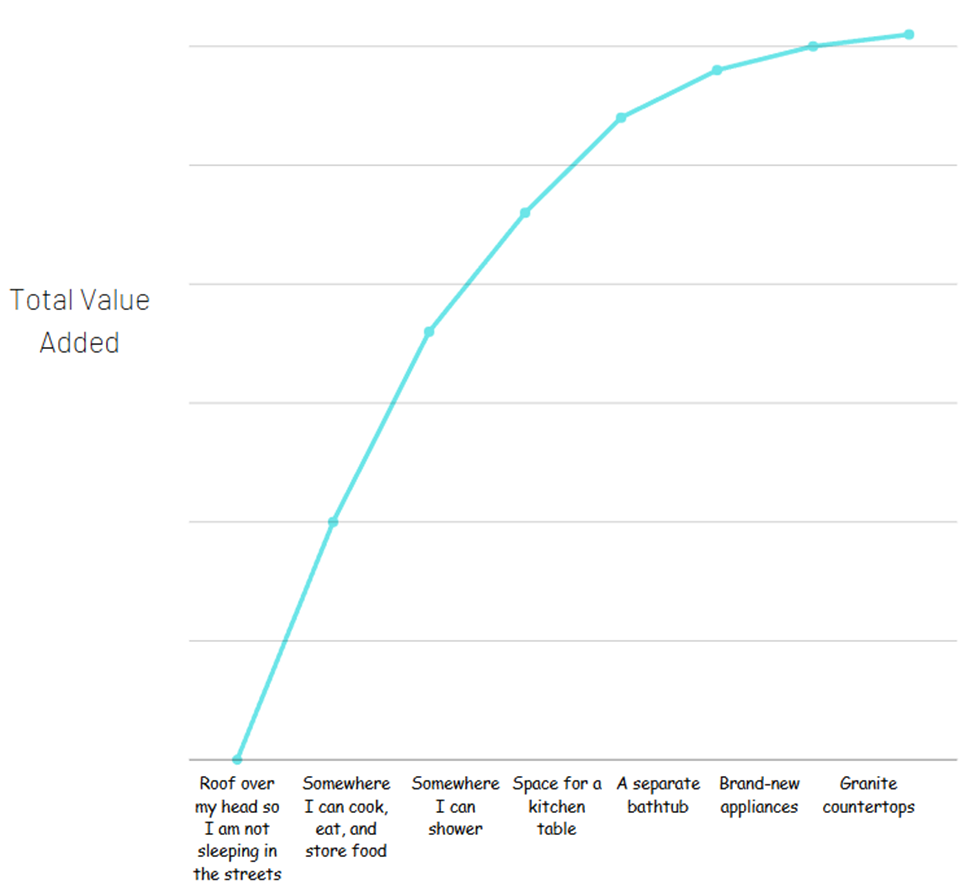
Οι περισσότερες από τις συνολικές αξίες προέρχονται από τα βασικά των βασικών. Αυτό δεν σημαίνει με κανέναν τρόπο ότι τα επιπλέον δεν αξίζουν – δεν υπάρχουν σημάδια δολαρίου εδώ, μόνο πόση αξία αποκτάτε.
Στην οικονομία, αυτή η έννοια ονομάζεται χρησιμότητα – η ικανοποίηση ή το όφελος που προκύπτει από την κατανάλωση αγαθών ή υπηρεσιών. Θα παρατηρήσετε ότι η καμπύλη ισιώνει καθώς οι δαπάνες αυξάνονται. Για να το μοντελοποιήσουμε μαθηματικά, χρησιμοποιούμε λογαρίθμους αντί για εκθέτες.
Τι είναι ο Λογάριθμος;
Μπορείτε να σκεφτείτε τους λογαρίθμους σε σχέση με τους εκθέτες με τον ίδιο τρόπο που η διαίρεση σχετίζεται με τον πολλαπλασιασμό – είναι η αντίθετη μαθηματική λειτουργία. Με άλλα λόγια,
Αν 2^3 = 8, τότε 3 είναι ο λογάριθμος του 8 με βάση το 2.
Στην οικονομία και τα χρηματοοικονομικά, οι λογαρίθμοι είναι χρήσιμοι για να δείξουν αυτές τις μειούμενες αποδόσεις κλίμακας για τις δαπάνες. Για παράδειγμα, αν θέλουμε να κάνουμε ένα γράφημα που να δείχνει τη χρησιμότητα που λαμβάνεται από την κατανάλωση κατά τη διάρκεια ενός συγκεκριμένου μήνα, το γράφημα μπορεί να φαίνεται έτσι:
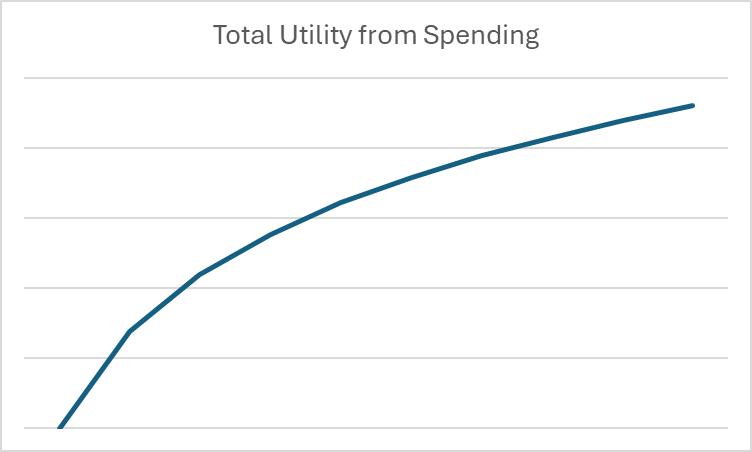
Μόλις βάλουμε τις δαπάνες μας στο πλαίσιο των λογαρίθμων και της χρησιμότητας, μπορούμε να αρχίσουμε να εξετάζουμε τις μακροχρόνιες αποφάσεις δαπανών και αποταμιεύσεων καθαρά μαθηματικά.
Χρονική Αξία του Χρήματος – Ποσοστά Έκπτωσης
Η Χρονική Αξία του Χρήματος αναφέρεται στο γεγονός ότι ένα δολάριο στο μέλλον αξίζει λιγότερο από ένα δολάριο σήμερα. Αυτό συμβαίνει επειδή μεταξύ τώρα και του μέλλοντος, θα μπορούσα να χρησιμοποιήσω αυτό το δολάριο για να κάνω κάτι – και αυτή η ευκαιρία μπορεί να έχει περάσει.
Όταν θέλουμε να περιγράψουμε μαθηματικά τη Χρονική Αξία του Χρήματος, χρησιμοποιούμε κάτι που ονομάζεται ποσοστό έκπτωσης. Το ποσοστό έκπτωσης είναι ένας απλός αριθμός μεταξύ 0 και 1 που απαντά σε αυτή την ερώτηση:
Πόσα θα θυσιάζατε σήμερα για να αποκτήσετε $1 σε 1 μήνα;

Το ποσοστό έκπτωσης κάθε ατόμου είναι διαφορετικό – αναφέρεται στο πόσο βραχυπρόθεσμες ή μακροπρόθεσμες είναι οι προσωπικές τους προτιμήσεις. Όπως μπορείτε να περιμένετε, ένα άτομο με υψηλό ποσοστό έκπτωσης (ας πούμε, 0.9) είναι πολύ πιο πιθανό να είναι αποταμιευτής από κάποιον με χαμηλό ποσοστό έκπτωσης (ας πούμε, 0.3). Αυτό συμβαίνει επειδή ένα άτομο με χαμηλό ποσοστό έκπτωσης εκτιμά πολύ το να έχει αυτά τα χρήματα τώρα – οπότε είναι πρόθυμο να θυσιάσει το 70% της αξίας του για να το αποκτήσει άμεσα αντί να περιμένει.
Το ποσοστό έκπτωσης συνήθως εκφράζεται με το ελληνικό γράμμα β. Έτσι, αν το προσωπικό σας ποσοστό έκπτωσης είναι 0.95, θα λέγαμε β = 0.95.
Ποσοστά Έκπτωσης και Εκθέτες
Μόλις μπορέσετε να προσδιορίσετε το προσωπικό σας ποσοστό έκπτωσης, μπορείτε επίσης να το χρησιμοποιήσετε για να υπολογίσετε πόσα θα δεχόσασταν για αυτό το δολάριο αν είναι ακόμα πιο μακριά στο μέλλον χρησιμοποιώντας εκθέτες.
Αυξάνοντας το β σας με έναν εκθέτη ίσο με το πόσο μακριά στο μέλλον θέλουμε να υπολογίσουμε, μπορούμε να πούμε πόσο αξίζει αυτό το δολάριο σήμερα. Με άλλα λόγια, β ^t = πόσα θα ήσασταν πρόθυμοι να δεχτείτε σήμερα σε αντάλλαγμα για ένα δολάριο t μήνες από τώρα.
Στο παράδειγμά μας με β = 0.95, αυτό είναι το πόσο αξίζει ένα δολάριο κατά τη διάρκεια του επόμενου έτους:
| Μήνες στο Μέλλον | Πόσο θα ήσασταν διατεθειμένοι να πάρετε σήμερα για να θυσιάσετε 1 $ στο μέλλον |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
Αυτό σημαίνει ότι αν το β σας = 0.95, θα ήσασταν διατεθειμένοι να πάρετε 0.54 $ για να θυσιάσετε ένα δολάριο σε ένα χρόνο από τώρα.
Τώρα που έχουμε την έννοια τόσο των λογαρίθμων όσο και των επιτοκίων, μπορούμε να τα συνδυάσουμε για να δούμε τι σημαίνει για τις αποφάσεις αποταμίευσης και δαπανών μακροπρόθεσμα!
Διαχρονική Χρησιμότητα
Οι περισσότερες από τις γνώσεις που αποκτάτε σε ένα μάθημα προσωπικών οικονομικών αφορούν την αποταμίευση για το μέλλον, ιδιαίτερα για τη σύνταξη. Αλλά αυτό δεν είναι πραγματικά ο χρηματοοικονομικός σας στόχος στη ζωή – πραγματικά θέλετε να μεγιστοποιήσετε τη συνολική διαχρονική σας χρησιμότητα. Γι’ αυτό κανείς δεν αποταμιεύει κάθε σεντ – ισορροπείτε το όφελος (ή τη χρησιμότητα) από τις δαπάνες σήμερα με την αύξηση του πλούτου σας (μέσω της δύναμης του σύνθετου επιτοκίου) ώστε να μπορείτε να το ξοδέψετε στο μέλλον.
Αυτό σημαίνει ότι κάθε μήνα της ζωής σας, έχετε το εισόδημά σας για εκείνο το μήνα, συν όλες τις αποταμιεύσεις που έχετε συσσωρεύσει μέχρι τότε. Αυτοί οι συνδυασμένοι πόροι είναι αυτοί με τους οποίους έχετε να εργαστείτε. Αποφασίζετε συνειδητά πόσο από αυτούς τους πόρους θα ξοδέψετε (ή θα καταναλώσετε) και πόσο θα αποταμιεύσετε (ή θα επενδύσετε). Έχετε επίσης κάποια κατανόηση του επιτοκίου με το οποίο οι αποταμιεύσεις σας θα αυξάνονται με την πάροδο του χρόνου. Με μαθηματικούς όρους, επιλέγετε c και i όπου:
I + (s x (1 + r)) = c + i
Όπου αυτές οι μεταβλητές αναφέρονται σε:
- I = το εισόδημά σας αυτό το μήνα
- s = πόσο έχετε ήδη αποταμιεύσει/επενδύσει στην αρχή του μήνα
- r = το επιτόκιο με το οποίο αυξάνονται οι αποταμιεύσεις σας. Έτσι, οι αποταμιεύσεις σας από τον προηγούμενο μήνα θα έχουν αυξηθεί λίγο περισσότερο μέχρι την αρχή αυτού του μήνα από ό,τι είχατε τον προηγούμενο μήνα.
- c = πόσο καταναλώνετε/ξοδεύετε αυτό το μήνα
- i = πόσο αποταμιεύετε/επενδύετε αυτό το μήνα
Το όφελος που αποκτάτε από την κατανάλωση μπορεί να εκφραστεί παίρνοντας τον λογάριθμο της κατανάλωσής σας:
Χρησιμότητα = log(c)
Πρέπει να προσδιορίσετε πόσο να ξοδέψετε (και κατά συνέπεια να αποταμιεύσετε) σε κάθε περίοδο για να μεγιστοποιήσετε τη συνολική διαχρονική σας χρησιμότητα, όχι μόνο την ευτυχία σας στην παρούσα στιγμή. Χρησιμοποιώντας το επιτόκιο σας και τους εκθέτες, μπορούμε να υπολογίσουμε τη χρησιμότητα που θα αποκτήσετε από την κατανάλωση σε οποιαδήποτε περίοδο στο μέλλον, και στη συνέχεια να τα προσθέσουμε όλα μαζί.
Συνολική Διαχρονική Χρησιμότητα =
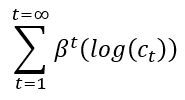
Όρια – Χρήσιμες και Εκπτώσεις Προσεγγίζουν το Μηδέν
Αρχικά, φαίνεται ότι αυτό μπορεί να είναι άπειρο – προσθέτουμε άπειρους αριθμούς, οπότε θα μπορούσε να γίνεται όλο και μεγαλύτερο για πάντα. Ωστόσο, επειδή t συνεχίζει να αυξάνεται, σημαίνει ότι η έκπτωση που εφαρμόζεται στο μακρινό μέλλον αρχίζει να πλησιάζει ΠΟΛΥ κοντά στο μηδέν.
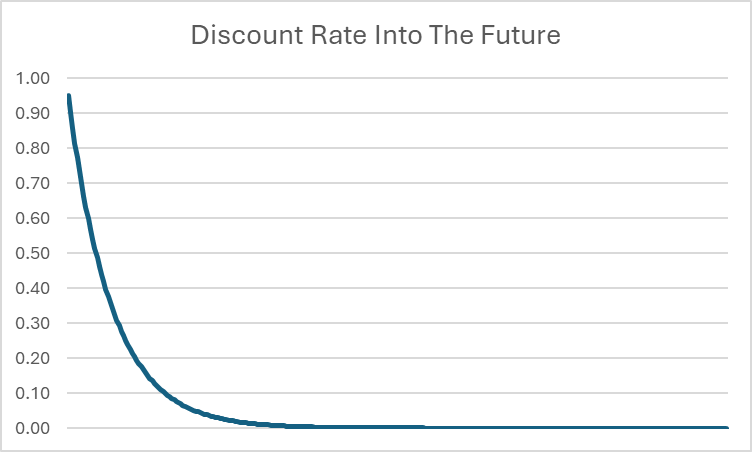
Για παράδειγμα, ακόμη και αν β = 0.95, ο ρυθμός έκπτωσης σε 20 χρόνια είναι μόλις 0.0000045. Όσο πιο μακριά πηγαίνει στο μέλλον, τόσο πιο κοντά στο 0 γίνεται ο ρυθμός έκπτωσης. Ενώ το ακριβές μέγιστο ποσό κατανάλωσης κατά τη διάρκεια της ζωής μπορεί να είναι αδύνατο να υπολογιστεί με απόλυτη ακρίβεια (καθώς θα μπορούσε θεωρητικά να περιλαμβάνει άπειρους δεκαδικούς αριθμούς), μπορούμε να δηλώσουμε με σιγουριά ότι υπάρχει ένα ανώτατο όριο στο συνολικό ποσό κατανάλωσης που μπορεί να επιτευχθεί κατά τη διάρκεια μιας ζωής.
Τα όρια χρησιμοποιούνται για να ορίσουν αυτά τα ανώτερα και κατώτερα όρια. Μπορούμε να πούμε με ασφάλεια ότι ο ρυθμός έκπτωσης έχει ένα κατώτατο όριο 0 καθώς t συνεχίζει να αυξάνεται προς το άπειρο – θα συνεχίσει να πλησιάζει το 0, αλλά ποτέ δεν θα το φτάσει. Το ανώτατο όριο της συνολικής χρησιμότητας κατά τη διάρκεια της ζωής μπορεί επίσης να υπολογιστεί (αλλά αυτό απαιτεί κάποια προχωρημένη ανάλυση, η οποία δεν είναι μέρος αυτού του μαθήματος).
Ρυθμοί Έκπτωσης και Ρυθμοί Επιτοκίων – Επιλέγοντας να Αποταμιεύσετε
Μόλις κοιτάξουμε πέρα από όλα τα μαθηματικά, αυτό που μπορούμε πραγματικά να δούμε είναι ότι η απόφαση να ξοδέψουμε ή να αποταμιεύσουμε βασίζεται πραγματικά σε μόνο δύο μεταβλητές:
- Ο προσωπικός σας ρυθμός έκπτωσης (ή β)
- Ο ρυθμός επιτοκίου r, ο οποίος καθορίζει πόσο θα αυξηθούν οι επενδύσεις σας
Αν υπάρχουν δύο άτομα που αναμένουν την ίδια απόδοση από τις επενδύσεις τους, αλλά παρατηρούμε ότι το ένα άτομο είναι μεγάλος αποταμιευτής και το άλλο μεγάλος ξοδευτής, μπορούμε να πούμε ότι ο αποταμιευτής έχει υψηλότερο β από τον ξοδευτή – μπορούμε να χρησιμοποιήσουμε έναν πραγματικό αριθμό για να ποσοτικοποιήσουμε ΠΟΣΟ αποταμιευτής ή ξοδευτής είναι κάποιος.

Μια ισχυρή κατανόηση των επιτοκίων είναι κρίσιμη για τη χρηματοοικονομική παιδεία. Αν η μόνη επιλογή αποταμίευσης είναι ένας λογαριασμός αποταμίευσης με χαμηλό επιτόκιο (ίσως κερδίζοντας μόνο 3% ετησίως), είναι λιγότερο πιθανό να δώσετε προτεραιότητα στους μακροπρόθεσμους στόχους αποταμίευσης. Αυτό συμβαίνει επειδή μπορεί να μην κατανοείτε πλήρως την προοπτική υψηλότερων κινδύνων και υψηλότερων αποδόσεων επενδύσεων όπως η χρηματιστηριακή αγορά.
Τελικά, η πιο σημαντική πτυχή της χρηματοοικονομικής παιδείας είναι να είστε ενήμεροι για τις επενδυτικές επιλογές που έχετε στη διάθεσή σας και να λαμβάνετε ενημερωμένες αποφάσεις με βάση τις ατομικές σας συνθήκες και την ανοχή σας στον κίνδυνο.