Δαπάνες κατά βούληση – Κατανόηση της Κεντρικής Τάσης
Τι είναι οι Δαπάνες κατά Βούληση;
Οι δαπάνες κατά βούληση είναι μη απαραίτητες αγορές— επιθυμίες, πράγματα που αγοράζουμε για ευχαρίστηση, ευκολία ή διασκέδαση. Παραδείγματα περιλαμβάνουν την ψυχαγωγία, το φαγητό έξω ή τα τελευταία τεχνολογικά γκάτζετ. Αντίθετα, ανάγκες είναι απαραίτητες για την επιβίωση: τροφή, στέγαση, υπηρεσίες κοινής ωφέλειας και υγειονομική περίθαλψη. Η κατανόηση της διαφοράς μεταξύ αναγκών και επιθυμιών είναι μια βασική χρηματοοικονομική δεξιότητα, ειδικά όταν αρχίσετε να διαχειρίζεστε τα δικά σας χρήματα.

Γιατί έχει σημασία
Η κατανόηση της διαφοράς μεταξύ αναγκών και επιθυμιών σας βοηθά να κάνετε πιο έξυπνες χρηματοοικονομικές επιλογές. Για παράδειγμα, αν έχετε αποταμιεύσει για ένα νέο βιντεοπαιχνίδι αλλά το τηλέφωνό σας σπάει, τι θα επιλέξετε; Το τηλέφωνο είναι ανάγκη; Το παιχνίδι είναι επιθυμία. Η επιλογή να αντικαταστήσετε το τηλέφωνο διασφαλίζει ότι καλύπτετε μια απαραίτητη δαπάνη, προετοιμάζοντάς σας για χρηματοοικονομική ασφάλεια μακροπρόθεσμα.
Ανάλυση Αναγκών vs. Επιθυμιών: Μια Δεδομένη Προσέγγιση
Η παρακολούθηση των δαπανών σας βοηθά να αποκαλύψετε πρότυπα στις χρηματοοικονομικές σας συνήθειες. Μπορείτε να παρακολουθήσετε πόσα ξοδεύετε εσείς και οι φίλοι σας σε μη απαραίτητα είδη όπως σνακ, ψυχαγωγία ή εφαρμογές. Εξετάζοντας αυτά τα δεδομένα, μπορείτε να αναλογιστείτε αν οι δαπάνες σας ευθυγραμμίζονται με τις προτεραιότητές σας.
Στην πραγματικότητα, έρευνες δείχνουν ότι οι άνθρωποι που σκέφτονται μακροπρόθεσμα τείνουν να αποταμιεύουν περισσότερα, ενώ αυτοί που επικεντρώνονται στην άμεση ικανοποίηση είναι πιο πιθανό να υπερβούν τις δαπάνες τους. Η ανάλυση των δεδομένων δαπανών σας μπορεί να σας βοηθήσει να πάρετε καλύτερες χρηματοοικονομικές αποφάσεις και να χτίσετε πιο υγιείς συνήθειες χρημάτων.
Χρησιμοποιώντας την Κεντρική Τάση για την Ανάλυση Δεδομένων Δαπανών
Όταν αναλύετε τις δαπάνες, τρία βασικά μέτρα κεντρικής τάσης—μέσος όρος, διάμεσος και συχνότητα—βοηθούν να συνοψίσουν τη χρηματοοικονομική σας συμπεριφορά:
- Μέσος Όρος: Ο μέσος όρος όλων των δαπανών σας. Αν και είναι χρήσιμος, ο μέσος όρος μπορεί να επηρεαστεί από ακραίες τιμές (όπως κάποιος που ξοδεύει πολύ περισσότερα ή λιγότερα από άλλους).
- Διάμεσος: Η μεσαία τιμή όταν όλα τα δεδομένα είναι τακτοποιημένα σε σειρά. Αυτό δίνει μια καλύτερη ιδέα για τις τυπικές δαπάνες αποφεύγοντας τις ακραίες τιμές.
- Συχνότητα: Η πιο συχνή τιμή. Αυτό μπορεί να βοηθήσει στην αναγνώριση κοινών συνηθειών ή δημοφιλών τάσεων στις δαπάνες.
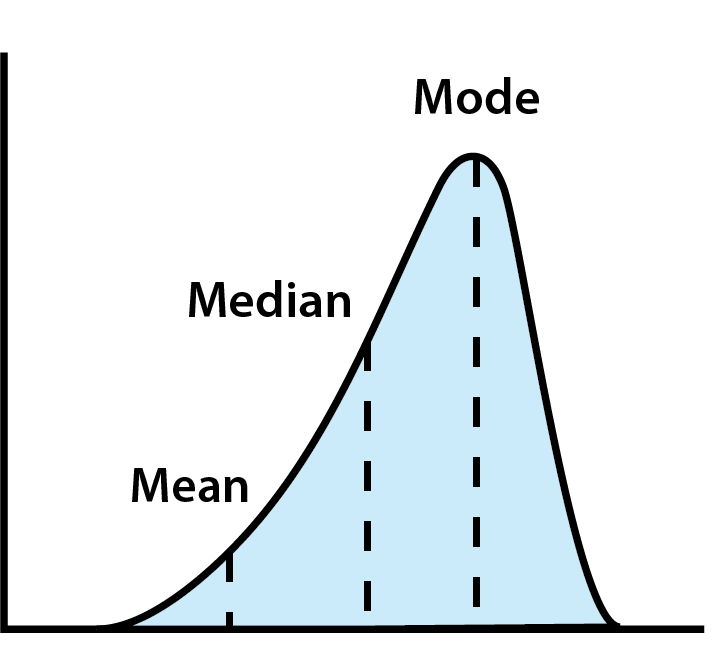
Χρησιμοποιώντας την Κεντρική Τάση για την Ανάλυση Δεδομένων Δαπανών
Η εξέταση της κεντρικής τάσης μπορεί να βοηθήσει να βάλετε τον προϋπολογισμό σας σε προοπτική. Για παράδειγμα, μπορεί να αγοράζετε έναν καφέ κάθε πρωί στο δρόμο για το σχολείο ή τη δουλειά. Συνειδητοποιείτε ότι αυτό μπορεί να προσθέσει, αλλά νομίζετε ότι ξοδεύετε περίπου όσο και ο επόμενος (ή η επόμενη), οπότε είναι μια λογική δαπάνη.
Αλλά αν ρωτήσετε μια ομάδα συνομηλίκων σας πόσα ξοδεύουν, μπορεί να σας δώσει μια μεγαλύτερη προοπτική για το πόσα ξοδεύετε πραγματικά κάθε μήνα.
- Μέσος Όρος: Αν ανακαλύψετε ότι ξοδεύετε περίπου όσο ο μέσος όρος, τότε είχατε δίκιο για τις δαπάνες σας. Αλλά αν διαπιστώσετε ότι ξοδεύετε πολύ περισσότερα από όλους τους άλλους, ίσως θελήσετε να ρίξετε μια πιο προσεκτική ματιά στις επιλογές ποτών σας.
- Διάμεσος: Ο διάμεσος σας λέει πώς οι ενέργειές σας ταιριάζουν με όλους τους άλλους. Ίσως αρκετοί άνθρωποι ξοδεύουν $0 για καφέ – αυτό θα επηρεάσει τον μέσο όρο χαμηλότερα από ό,τι ξοδεύει ο τυπικός καταναλωτής καφέ. Σε αυτή την περίπτωση, μπορεί να δείτε ότι ξοδεύετε λιγότερα από τον διάμεσο, οπότε οι δαπάνες σας είναι πράγματι λογικές.
- Συχνότητα: Η πιο συχνή τιμή. Ίσως μια ομάδα φίλων παραγγέλνει τον ίδιο Orange Mocha Frappuccino κάθε πρωί – κάνοντάς τον την πιο συχνή επιλογή. Αν γνωρίζετε ότι ο Orange Mocha Frappuccino είναι ακριβός, μπορεί να σημαίνει ότι ο διάμεσος είναι επίσης επηρεασμένος υψηλότερα από ό,τι νομίζετε ότι παραγγέλνει ο τυπικός καταναλωτής καφέ.
Παράδειγμα: Η Συνήθεια Καφέ του Esteban
Ο Esteban αγοράζει έναν καφέ $4.75 κάθε πρωί. Ενώ πιστεύει ότι αυτή είναι μια λογική τιμή, είναι περίεργος να μάθει αν είναι τυπική. Για να αποκτήσει μια καλύτερη αίσθηση του μέσου κόστους, ρωτά τους φίλους, την οικογένεια και τους συναδέλφους του πόσα ξόδεψαν για τον πρωινό καφέ τους. Αυτές είναι οι απαντήσεις τους:

| Απαντητής | Πόσα Ξόδεψαν Αυτό το Πρωί |
|---|---|
| 1 | $0.00 |
| 2 | $6.95 |
| 3 | $1.99 |
| 4 | $0.00 |
| 5 | $4.25 |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. Υπολογισμός του Μέσου Όρου
Αρχικά, ο Esteban θέλει να δοκιμάσει την πρώτη του υπόθεση – ότι ξοδεύει περίπου το μέσο όρο όλων των άλλων. Έτσι, θα υπολογίσει τον μέσο όρο, ή αλλιώς το μέσο. Ο τύπος για τον υπολογισμό του μέσου είναι:
Μέσος = άθροισμα παρατηρήσεων / πλήθος παρατηρήσεων
Ο τύπος μπορεί επίσης να γραφτεί σε αυτό που ονομάζεται Σημειογραφία Σίγμα:
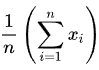
Με τη Σημειογραφία Σίγμα, το σήμα Σίγμα (Σ) σημαίνει “πρόσθεση”, το n σημαίνει πόσες παρατηρήσεις, το x σημαίνει για μια συγκεκριμένη παρατήρηση, και το i σημαίνει για κάθε παρατήρηση. Έτσι, αυτό που λέει είναι ότι από την πρώτη (i = 1, στο κάτω μέρος του σίγμα) μέχρι την τελευταία παρατήρηση (στο n, που είναι στην κορυφή του σίγμα), προσθέστε όλες τις τιμές τους, και στη συνέχεια πολλαπλασιάστε με 1/n. Η Σημειογραφία Σίγμα είναι πολύ κοινή στους ερευνητικούς τομείς, καθώς δείχνει αλγεβρικές ή μαθηματικές λειτουργίες που εφαρμόζονται σε μια ολόκληρη σειρά αριθμών, αντί για έναν κάθε φορά.
Έτσι, προσθέτουμε όλες τις παρατηρήσεις:
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
Και διαιρούμε με 15 (πλήθος παρατηρήσεων)
$78.10 / 15 = $5.21
Ο Esteban είχε δίκιο – ξοδεύει λιγότερο από τον μέσο όρο. Το $4.75 του είναι φθηνότερο από την μέση τιμή των $5.21.
2. Υπολογισμός της Διάμεσου
Για να υπολογίσουμε τη διάμεσο, πρέπει να αναδιατάξουμε τις παρατηρήσεις από την μικρότερη στην μεγαλύτερη. Η διάμεσος είναι ο μεσαίος αριθμός.
| Απαντητής | Πόσα Ξόδεψαν Αυτό το Πρωί |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
Η μεσαία τιμή (διάμεσος) των πρωινών εξόδων καφέ των φίλων, της οικογένειας και των συνεργατών του είναι στην πραγματικότητα $3.00, σημαντικά χαμηλότερη από το $4.75 του Esteban. Αυτή η ανακάλυψη κάνει τον Esteban να αισθάνεται λιγότερο άνετα με τη συνήθεια του καθημερινού καφέ του. Συνειδητοποιεί ότι ξοδεύει 50% περισσότερα από τους συνομηλίκους του, αν και το ατομικό του κόστος είναι κάτω από την μέση τιμή.
3. Υπολογισμός της Κατανομής
Τέλος, ο Esteban θέλει να δει ποια είναι η πιο δημοφιλής επιλογή. Για αυτό, πρέπει να βρει την κατανομή. Η κατανομή είναι απλώς η πιο κοινή παρατήρηση. Στην περίπτωση της έρευνάς του, 5 άτομα απάντησαν $0.00 – κάνοντάς το αυτή την πιο κοινή επιλογή (την κατανομή). Αν και δεν είναι η πλειοψηφία των ανθρώπων, αυτό σίγουρα έχει μεγάλο αντίκτυπο στους μέσους και τις διαμεσότητες επιλογές. Ο Esteban δεν είναι σίγουρος τι να κάνει με αυτές τις πληροφορίες – αλλά υπάρχει περισσότερη μαθηματική βοήθεια για να βρει μια απάντηση!
Ερμηνεία των Δεδομένων: Ασυμμετρία, Ακραίες Τιμές και Κατανομές
Ο Εστέμπαν εξετάζει προβλήματα στην ανάλυσή του που προέρχονται από την κατανομή των απαντήσεών του – ή πώς φαίνονται οι απαντήσεις του σε ένα γράφημα.
Ασυμμετρία
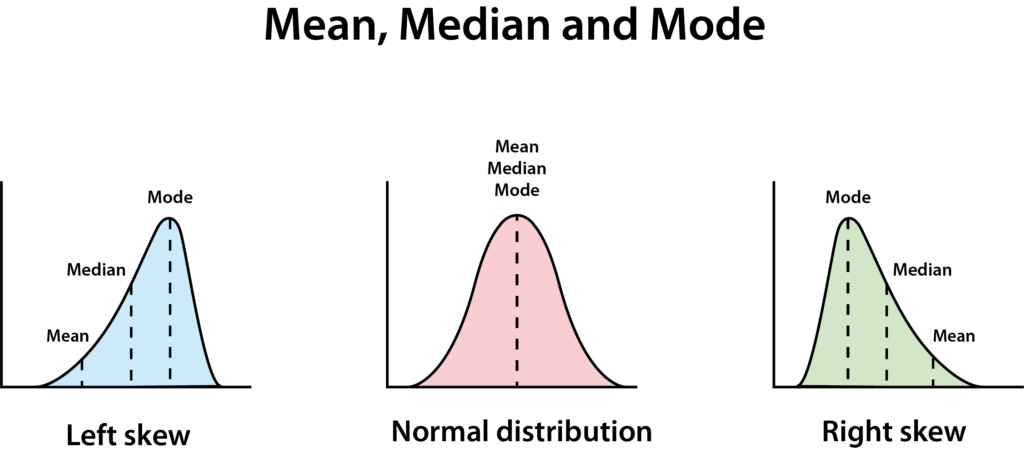
Μια κανονική κατανομή έχει καθαρό σχήμα καμπάνας. Μια τέλεια κανονική κατανομή έχει ως αποτέλεσμα τον μέσο όρο, τη διάμεσο και τη συχνότητα να είναι όλοι ίσοι.
Αν δεν είναι όλοι ίσοι, σημαίνει ότι τα δεδομένα είναι ασύμμετρα – σε αυτή την περίπτωση, λέμε ότι τα δεδομένα του έχουν μια κατανομή με δεξιά ασυμμετρία, που σημαίνει ότι η διάμεσος είναι χαμηλότερη από τον μέσο όρο. Αυτό συμβαίνει συχνά όταν υπάρχουν λίγοι πραγματικά μεγάλοι ή πραγματικά μικροί αριθμοί, κάνοντάς το γράφημα να φαίνεται ότι έχει μια μακριά κλίση προς τα δεξιά.
Ακραίες τιμές
Όταν ο Εστέμπαν εξετάζει προσεκτικά τις απαντήσεις, παρατηρεί μια ακραία τιμή: ένα κόστος $24.68. Αυτή η τιμή είναι σημαντικά υψηλότερη από οποιαδήποτε άλλη. Οι ακραίες τιμές είναι δεδομένα που απέχουν πολύ από την υπόλοιπη ομάδα και συχνά αποκλείονται από στατιστική ανάλυση επειδή μπορούν να παραμορφώσουν τα αποτελέσματα.
Μετά από περαιτέρω έρευνα, ο Εστέμπαν μαθαίνει ότι αυτή η ακραία τιμή αντιπροσωπεύει το κόστος ενός γαλονιού φρεσκοστυμμένου χυμού πορτοκαλιού που αγοράστηκε για ολόκληρη την οικογένεια αυτού του ατόμου το πρωί. Αυτή η δαπάνη δεν είναι σαφώς συγκρίσιμη με το τυπικό κόστος ενός μόνο φλιτζανιού καφέ.
Διπλές κατανομές
Διπλές κατανομές συμβαίνουν όταν κοιτάτε την κατανομή συχνότητας και δεν βλέπετε μόνο μία κορυφή, αλλά δύο (ή περισσότερες). Ρίξτε μια ματιά σε αυτές τις απαντήσεις από έρευνα σχετικά με το πόσα πλήρωσαν οι μαθητές λυκείου για τα γεύματά τους σε μια συγκεκριμένη ημέρα:
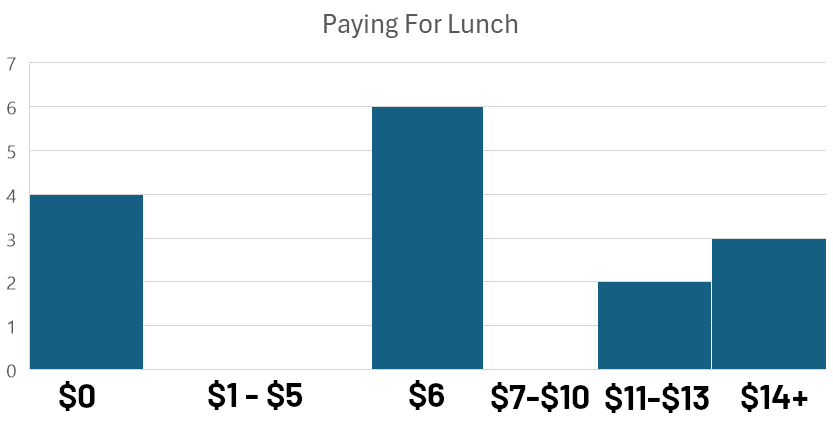
Αυτός ο τύπος γραφήματος, όπου τα δεδομένα ομαδοποιούνται σε διαστήματα ή ‘δοχεία’ για οπτική σύγκριση, ονομάζεται ιστόγραμμα. Η ανάλυση του πώς οι παρατηρήσεις κατανέμονται μέσα σε αυτά τα δοχεία είναι γνωστή ως ανάλυση συχνότητας.
Παρατηρώντας το ιστόγραμμα, παρατηρούμε δύο διακριτές κορυφές: μία κοντά στο $0 και μία άλλη κοντά στο $6. Αυτή η διπλή κατανομή (με κορυφές κοντά στο $0 και $6) υποδηλώνει ότι υπάρχουν δύο διακριτές ομάδες μέσα στα δεδομένα.
Η αναγνώριση αυτών των κορυφών μπορεί να καθοδηγήσει περαιτέρω έρευνα θέτοντας ερωτήσεις όπως:
- Ποιους παράγοντες μπορεί να εξηγήσουν αυτά τα δύο διακριτά πρότυπα δαπανών;
- Τι αποκαλύπτουν αυτές οι κορυφές σχετικά με τα υποκείμενα κίνητρα και τις συμπεριφορές των ατόμων σε αυτές τις ομάδες;
Επιπλέον, η παρουσία αυτών των δύο κορυφών υποδηλώνει μια κατανομή με δεξιά ασυμμετρία, που σημαίνει ότι μια μεγαλύτερη αναλογία των δεδομένων είναι συγκεντρωμένη προς το χαμηλότερο άκρο της κλίμακας τιμών.
Διπλά δεδομένα δεν σημαίνει απαραίτητα ότι υπάρχουν δύο απαντήσεις με τον ακριβή ίδιο αριθμό παρατηρήσεων, απλώς ότι μπορούμε να δούμε δύο καθαρές κορυφές (σε αυτή την περίπτωση το $6 είναι η “Αληθινή Κορυφή”).
Όταν οι ερευνητές κοίταξαν πιο προσεκτικά τα δεδομένα, η εξήγηση έγινε προφανής. Το $0 ήταν οι μαθητές που έφεραν το γεύμα τους από το σπίτι και το $6 ήταν το κόστος του κανονικού σχολικού γεύματος. Οι μαθητές που πλήρωσαν περισσότερα από $10 αγόραζαν έναν συνδυασμό προϊόντων από το σνακ μπαρ του σχολείου και άλλων τροφίμων που αγόρασαν στο δρόμο για το σχολείο.

Συμπέρασμα: Χρησιμοποιώντας Δεδομένα για Καλύτερες Οικονομικές Αποφάσεις
Κατανοώντας αυτά τα τρία μέτρα κεντρικής τάσης: μέσος όρος, διάμεσος και συχνότητα, μπορείτε να ερμηνεύσετε δεδομένα και να κάνετε πιο ενημερωμένες οικονομικές επιλογές. Είτε αναλύετε τις δαπάνες σας είτε εξετάζετε μεγαλύτερες τάσεις, αυτά τα εργαλεία σας δίνουν τη δυνατότητα να αναπτύξετε καλύτερες συνήθειες χρημάτων. Η συλλογή και ανάλυση δεδομένων δαπανών μπορεί να παρέχει πληροφορίες σχετικά με τη χρηματοοικονομική σας συμπεριφορά.
Για μαθητές όπως ο Εστέμπαν, απλές αλλαγές—όπως η μείωση των διακριτικών αγορών—μπορούν να οδηγήσουν σε μακροπρόθεσμα οικονομικά οφέλη. Όταν ο Εστέμπαν βλέπει ότι οι δαπάνες του είναι πάνω από τη διάμεσο – και ότι η πιο δημοφιλής επιλογή είναι να μην ξοδέψει καθόλου, αυτό βοηθά να βάλει σε πλαίσιο τις αποφάσεις δαπανών του και τι σημαίνει αυτό για το μέλλον του.