Grenzen und Protokolle – Personalisierte Ausgaben und Ersparnisse
Ein großer Teil der persönlichen Finanzen konzentriert sich auf langfristiges Denken: Ihr Budget so zu gestalten, dass Sie genug Geld sparen können, um den Lebensstil zu führen, den Sie möchten, und bequem in den Ruhestand zu gehen.
Aber für jede einzelne Person können „ein Lebensstil, den Sie wollen“ und „bequem in den Ruhestand gehen“ sehr unterschiedliche Dinge bedeuten. Am Ende des Tages trifft jede Person jeden Monat eine Entscheidung darüber, wie viel sie ausgeben (oder konsumieren) und wie viel sie sparen (oder investieren) wird.
Indem Sie den Denkprozess hinter diesem Trade-off verstehen, können Sie ein klareres Bild Ihrer eigenen Ausgaben gewinnen. Dies wird Ihnen helfen, sicherzustellen, dass Ihre tatsächlichen Ausgaben mit Ihren beabsichtigten Ausgaben übereinstimmen.
Modellierung des Konsums – Abnehmende Skalenerträge
Ein großer Teil der Finanzmathematik konzentriert sich auf exponentielles Wachstum – wie eine Investition basierend auf einem Zinssatz wächst, wie ein Sparkonto im Laufe der Zeit wächst oder wie man langfristigen Wohlstand aufbaut. Exponentielle Funktionen haben eine aufwärts gerichtete Kurve – Investitionen werden im Laufe der Zeit größer:

Aber wenn Sie ausgeben statt sparen, hat der Nutzen, den Sie für jeden Dollar, den Sie ausgeben, erhalten, nicht diese aufwärts gerichtete Kurve. Stattdessen sagen Ökonomen, dass der Konsum abnehmende Skalenerträge hat.
Denken Sie so darüber nach – Sie sehen zwei Wohnungen zur Miete. Eine hat ein Schlafzimmer, die Geräte sind 30 Jahre alt, das Badezimmer ist winzig und die Küche hat nicht einmal Platz für einen Tisch. Diese Wohnung wird für 500 $ / Monat Miete angeboten.
Die zweite Wohnung hat brandneue Geräte, ein geräumiges Badezimmer mit separater Badewanne und Dusche, und die Küche hat Granit-Arbeitsplatten mit Platz für einen Tisch und eine Frühstücksbar. Diese wird für 1.500 $ / Monat Miete angeboten.
Jetzt könnte die zweite Wohnung durchaus 1.000 $ mehr pro Monat wert sein. Aber der Wert, den Sie für eine Wohnung erhalten (ein Ort zum Schlafen in der Nacht, Ihre Sachen sicher zu lagern, Essen zu kochen und zu essen usw.), ist der wichtigste Teil. Wenn Sie versuchen würden, alle verschiedenen Annehmlichkeiten, die Sie mit der teureren Wohnung erhalten, zu trennen, um zu sehen, woher der gesamte Wert kommt, könnte es so aussehen:
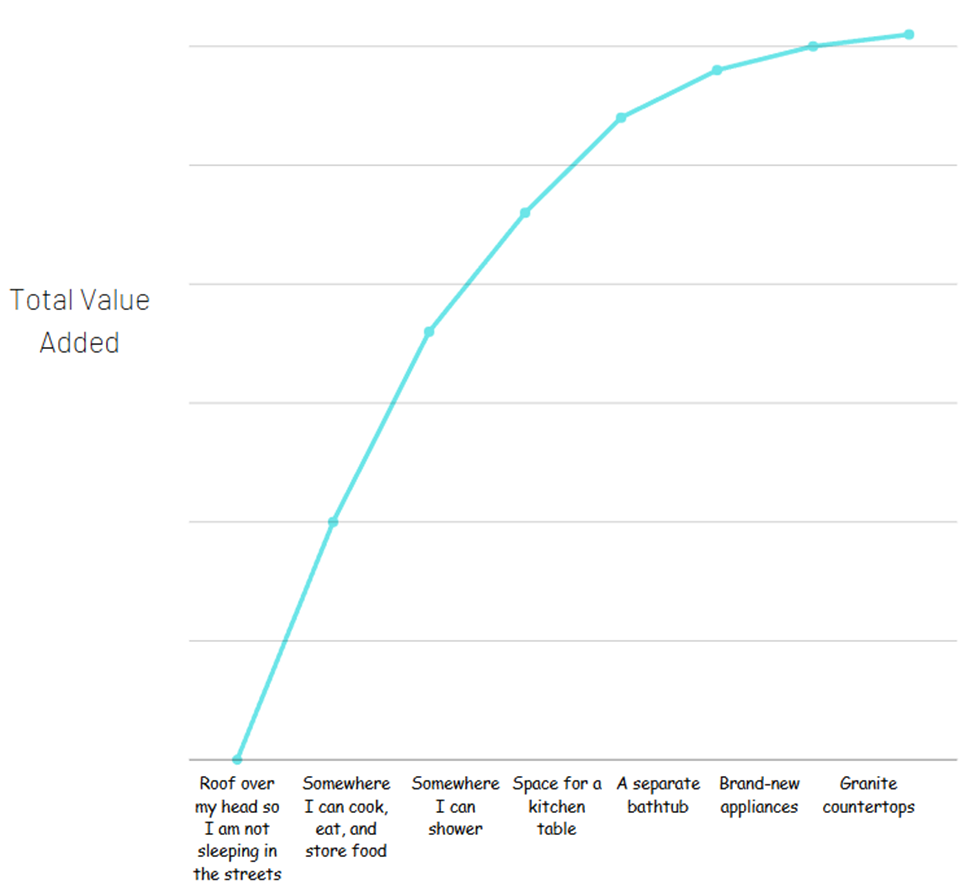
Der größte Teil des Gesamtwerts stammt von den Grundlagen der Grundlagen. Das bedeutet keineswegs, dass die Extras nicht wertvoll sind – hier gibt es keine Dollarzeichen, nur wie viel Wert Sie erhalten.
In der Wirtschaft wird dieses Konzept Nutzwert genannt – die Zufriedenheit oder der Nutzen, der aus dem Konsum von Gütern oder Dienstleistungen resultiert. Sie werden feststellen, dass die Kurve abflacht, wenn die Ausgaben steigen. Um dies mathematisch zu modellieren, verwenden wir Logarithmen anstelle von Exponenten.
Was ist ein Logarithmus?
Sie können sich Logarithmen in Bezug auf Exponenten so vorstellen, wie Division mit Multiplikation zusammenhängt – es ist die entgegengesetzte mathematische Funktion. Mit anderen Worten,
Wenn 2^3 = 8, dann ist 3 der Logarithmus von 8 zur Basis 2.
In der Wirtschaft und Finanzen sind Logarithmen nützlich, um diese abnehmenden Skalenerträge für Ausgaben zu zeigen. Wenn wir beispielsweise ein Diagramm erstellen möchten, das den Nutzen zeigt, der aus dem Konsum in einem bestimmten Monat resultiert, könnte das Diagramm so aussehen:
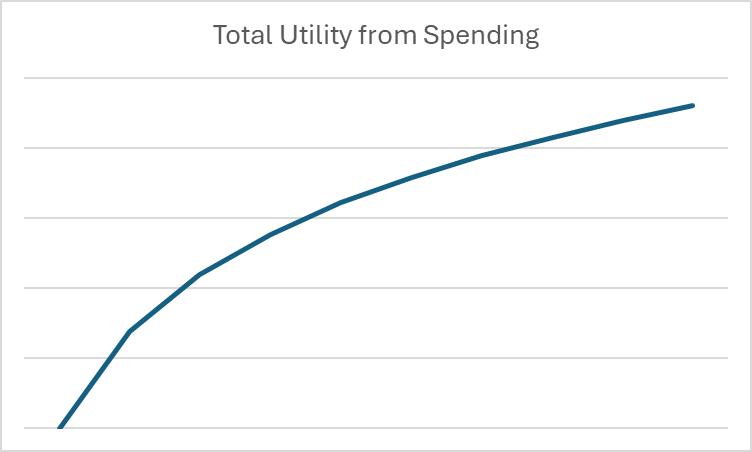
Sobald wir unsere Ausgaben im Kontext von Logarithmen und Nutzen betrachten, können wir beginnen, langfristige Ausgaben- und Sparentscheidungen rein mathematisch zu betrachten.
Zeitwert des Geldes – Diskontsatz
Der Zeitwert des Geldes bezieht sich auf die Tatsache, dass ein Dollar in der Zukunft weniger wert ist als ein Dollar heute. Das liegt daran, dass ich zwischen jetzt und der Zukunft diesen Dollar hätte verwenden können, um etwas zu tun – und diese Gelegenheit könnte vergangen sein.
Wenn wir den Zeitwert des Geldes mathematisch beschreiben möchten, verwenden wir etwas, das als Diskontsatz bezeichnet wird. Der Diskontsatz ist eine einfache Zahl zwischen 0 und 1, die diese Frage beantwortet:
Wie viel würden Sie heute aufgeben, um in einem Monat 1 $ zu erhalten?

Der Diskontsatz jeder Person ist unterschiedlich – er bezieht sich darauf, wie kurzfristig oder langfristig ihre persönlichen Präferenzen sind. Wie Sie vielleicht erwarten, ist eine Person mit einem hohen Diskontsatz (sagen wir, 0,9) viel wahrscheinlicher ein Sparer als jemand mit einem niedrigen Diskontsatz (sagen wir, 0,3). Das liegt daran, dass eine Person mit einem niedrigen Diskontsatz sehr viel Wert darauf legt, dieses Geld jetzt zu haben – sie sind also bereit, 70 % seines Wertes aufzugeben, um es sofort zu erhalten, anstatt zu warten.
Der Diskontsatz wird normalerweise mit dem griechischen Buchstaben β ausgedrückt. Wenn Ihr persönlicher Diskontsatz also 0,95 beträgt, würden wir sagen β = 0,95.
Diskontsatz und Exponenten
Sobald Sie Ihren eigenen persönlichen Diskontsatz identifizieren können, können Sie ihn auch verwenden, um herauszufinden, wie viel Sie für diesen Dollar verlangen würden, wenn er noch weiter in der Zukunft liegt indem Sie Exponenten verwenden.
Indem Sie Ihr Beta um einen Exponenten erhöhen, der angibt, wie weit in der Zukunft wir berechnen möchten, können wir sagen, wie viel dieser Dollar heute wert ist. Mit anderen Worten, β ^t = wie viel Sie heute bereit wären, im Austausch für einen Dollar t Monate von jetzt an zu nehmen.
In unserem Beispiel von β = 0.95 ist dies, was ein Dollar im nächsten Jahr wert ist:
| Monate in der Zukunft | Wie viel Sie heute bereit wären zu nehmen, um $1 in der Zukunft zu opfern |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
Das bedeutet, dass wenn Ihr β = 0.95 ist, Sie bereit wären, $0.54 zu nehmen, um einen Dollar in einem Jahr zu opfern.
Jetzt, da wir das Konzept von Logarithmen und Diskontsatz verstanden haben, können wir es zusammenfügen, um zu sehen, was es für langfristige Spar- und Ausgabenentscheidungen bedeutet!
Lebenszeitnutzwert
Das meiste, was Sie in einem Kurs über persönliche Finanzen lernen, dreht sich darum, für die Zukunft zu sparen, insbesondere für die Rente. Aber das ist nicht wirklich Ihr finanzielles Ziel im Leben – Sie möchten wirklich Ihren gesamten Lebensnutzwert maximieren. Deshalb spart niemand jeden Cent – Sie balancieren Ihren Nutzen (oder Nutzen) aus, den Sie heute durch Ausgaben erhalten, gegen das Wachstum Ihres Vermögens (durch die Kraft des Zinseszinses), damit Sie es in der Zukunft ausgeben können.
Das bedeutet, dass Sie jeden Monat Ihres Lebens Ihr Einkommen für diesen Monat haben, plus all die Ersparnisse, die Sie bis dahin angesammelt haben. Diese kombinierten Ressourcen sind das, womit Sie arbeiten müssen. Sie entscheiden bewusst, wie viel von diesen Ressourcen Sie ausgeben (oder konsumieren) und wie viel Sie sparen (oder investieren) werden. Sie haben auch ein gewisses Verständnis für den Zinssatz, zu dem Ihre Ersparnisse im Laufe der Zeit wachsen werden. Mathematisch gesehen wählen Sie c und i, wobei:
I + (s x (1 + r)) = c + i
Wo sich diese Variablen auf Folgendes beziehen:
- I = Ihr Einkommen in diesem Monat
- s = wie viel Sie bereits zu Beginn des Monats gespart/investiert haben
- r = der Zinssatz, zu dem Ihre Ersparnisse wachsen. Ihre Ersparnisse vom letzten Monat werden zu Beginn dieses Monats ein wenig mehr gewachsen sein als im letzten Monat.
- c = wie viel Sie in diesem Monat konsumieren/ausgeben
- i = wie viel Sie in diesem Monat sparen/investieren
Der Nutzen, den Sie aus dem Konsum ziehen, kann ausgedrückt werden, indem Sie den Logarithmus Ihres Konsums nehmen:
Nutzen = log(c)
Sie müssen bestimmen, wie viel Sie in jedem Zeitraum ausgeben (und folglich sparen), um Ihren gesamten Lebensnutzwert zu maximieren, nicht nur Ihr Glück im gegenwärtigen Moment. Mit Ihrem Diskontsatz und Exponenten können wir den Nutzen berechnen, den Sie aus dem Konsum in jedem zukünftigen Zeitraum erhalten, und dann alles zusammenzählen.
Gesamter Lebensnutzwert =
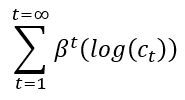
Grenzen – Nutzen und Rabatte nähern sich Null
Auf den ersten Blick scheint es, als könnte dies unendlich sein – wir addieren unendliche Zahlen, also könnte es immer größer werden. Da jedoch t weiter wächst, bedeutet das, dass der in der Zukunft angewandte Rabatt sehr nahe an null kommt.
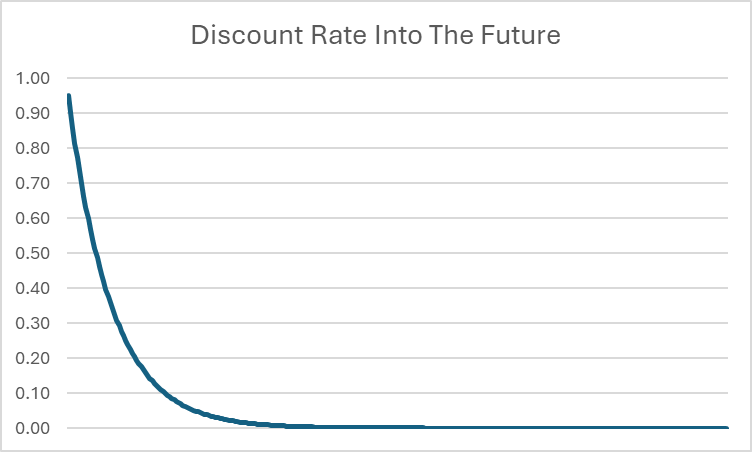
Zum Beispiel, selbst wenn β = 0,95 ist, liegt der Rabatt in 20 Jahren bei nur 0,0000045. Je weiter in die Zukunft es geht, desto näher kommt der Rabatt auf 0. Während die genaue maximale Menge an Lebenszeitkonsum möglicherweise unmöglich mit absoluter Präzision zu berechnen ist (da sie theoretisch eine unendliche Anzahl von Dezimalstellen beinhalten könnte), können wir mit Zuversicht sagen, dass es eine obere Grenze für die insgesamt über ein Leben hinweg erreichbare Konsummenge gibt.
Grenzen werden verwendet, um diese oberen und unteren Grenzen zu definieren. Wir können mit Sicherheit sagen, dass der Rabatt eine untere Grenze von 0 hat, während t weiter gegen unendlich wächst – er wird sich 0 nähern, aber niemals erreichen. Die obere Grenze des gesamten Lebensnutzens kann ebenfalls berechnet werden (aber dies erfordert einige fortgeschrittene Mathematik, die nicht Teil dieser Lektion ist).
Rabatt- und Zinssätze – Entscheidung zum Sparen
Wenn wir über die gesamte Mathematik hinwegsehen, sehen wir, dass die Entscheidung, auszugeben oder zu sparen, wirklich nur auf zwei Variablen basiert:
- Ihr eigener persönlicher Rabatt (oder β)
- Der Zinssatz r, der bestimmt, wie viel Ihre Investitionen wachsen werden
Wenn es zwei Personen gibt, die die gleiche Rendite auf ihre Ersparnisse erwarten, wir aber beobachten, dass eine Person ein großer Sparer und die andere ein großer Ausgeber ist, können wir sagen, dass der Sparer ein höheres β hat als der Ausgeber – wir können eine tatsächliche Zahl verwenden, um zu quantifizieren, WIE VIEL ein Sparer oder Ausgeber jemand ist.

Ein starkes Verständnis von Zinssätzen ist entscheidend für die finanzielle Bildung. Wenn Ihre einzige Sparoption ein niedrig verzinstes Sparkonto ist (vielleicht nur 3 % jährlich), werden Sie weniger wahrscheinlich langfristige Sparziele priorisieren. Das liegt daran, dass Sie möglicherweise das Potenzial höherer Risiken und höherer Renditen, wie sie der Aktienmarkt bietet, nicht vollständig verstehen.
Letztendlich ist der wichtigste Aspekt der finanziellen Bildung, sich der verfügbaren Investitionsmöglichkeiten bewusst zu sein und informierte Entscheidungen basierend auf Ihren individuellen Umständen und Ihrer Risikobereitschaft zu treffen.