Discretionäre Ausgaben – Verständnis der zentralen Tendenz
Was sind discretionary expenses?
Discretionäre Ausgaben sind nicht essentielle Käufe – Wünsche, Dinge, die wir zum Vergnügen, zur Bequemlichkeit oder zum Spaß kaufen. Beispiele sind Unterhaltung, Essen gehen oder die neuesten technischen Geräte. Im Gegensatz dazu sind Bedürfnisse für das Überleben unerlässlich: Nahrung, Unterkunft, Versorgungsleistungen und Gesundheitsversorgung. Den Unterschied zwischen Bedürfnissen und Wünschen zu kennen, ist eine wichtige finanzielle Fähigkeit, insbesondere wenn Sie anfangen, Ihr eigenes Geld zu verwalten.

Warum es wichtig ist
Den Unterschied zwischen Bedürfnissen und Wünschen zu verstehen, hilft Ihnen, klügere finanzielle Entscheidungen zu treffen. Wenn Sie beispielsweise für ein neues Videospiel gespart haben, aber Ihr Telefon kaputt geht, was wählen Sie? Das Telefon ist ein Bedürfnis; das Spiel ist ein Wunsch. Sich für den Austausch des Telefons zu entscheiden, stellt sicher, dass Sie eine notwendige Ausgabe decken, was Ihnen langfristige finanzielle Sicherheit verschafft.
Bedürfnisse vs. Wünsche analysieren: Ein datenbasierter Ansatz
Ihr Ausgabeverhalten zu verfolgen, hilft, Muster in Ihren finanziellen Gewohnheiten zu erkennen. Sie könnten verfolgen, wie viel Sie und Ihre Freunde für nicht essentielle Dinge wie Snacks, Unterhaltung oder Apps ausgeben. Durch die Untersuchung dieser Daten können Sie reflektieren, ob Ihre Ausgaben mit Ihren Prioritäten übereinstimmen.
Tatsächlich zeigen Forschungen, dass Menschen, die langfristig denken, tendenziell mehr sparen, während diejenigen, die auf sofortige Befriedigung fokussiert sind, eher dazu neigen, zu viel auszugeben. Ihre Ausgabedaten zu analysieren, kann Ihnen helfen, bessere finanzielle Entscheidungen zu treffen und gesündere Geldgewohnheiten zu entwickeln.
Zentrale Tendenz zur Analyse von Ausgabedaten verwenden
Bei der Analyse von Ausgaben helfen drei wichtige Maße der zentralen Tendenz – Mittelwert, Median und Modus – Ihr finanzielles Verhalten zusammenzufassen:
- Mittelwert: Der Durchschnitt aller Ihrer Ausgaben. Obwohl nützlich, kann der Mittelwert durch extreme Werte (wie jemand, der viel mehr oder weniger ausgibt als andere) verzerrt werden.
- Median: Der Mittelwert, wenn alle Daten in Reihenfolge angeordnet sind. Dies gibt eine bessere Vorstellung von typischen Ausgaben, indem Ausreißer vermieden werden.
- Modus: Der häufigste Wert. Dies kann helfen, gängige Gewohnheiten oder beliebte Trends im Ausgabeverhalten zu identifizieren.
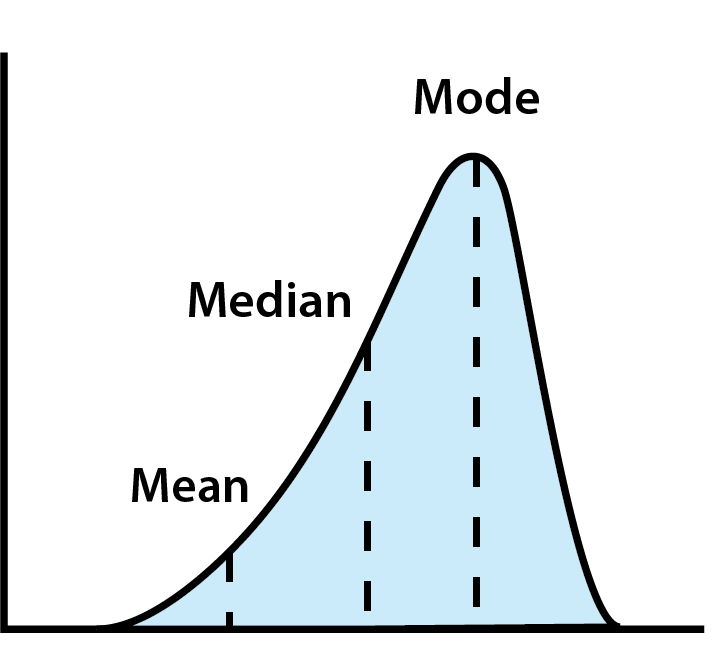
Zentrale Tendenz zur Analyse von Ausgabedaten verwenden
Die Betrachtung der zentralen Tendenz kann helfen, Ihr eigenes Budget in Perspektive zu setzen. Wenn Sie beispielsweise jeden Morgen auf dem Weg zur Schule oder zur Arbeit einen Kaffee kaufen, erkennen Sie, dass sich das summieren kann, aber Sie denken, dass Sie etwa so viel ausgeben wie der nächste (oder die nächste), also ist es eine angemessene Ausgabe.
Wenn Sie jedoch eine Gruppe Ihrer Altersgenossen fragen, wie viel sie ausgeben, kann Ihnen das eine größere Perspektive darauf geben, wie viel Sie tatsächlich jeden Monat ausgeben.
- Mittelwert: Wenn Sie herausfinden, dass Sie etwa so viel ausgeben wie der Durchschnitt, dann hatten Sie recht mit Ihren eigenen Ausgabengewohnheiten. Wenn Sie jedoch feststellen, dass Sie viel mehr ausgeben als alle anderen, sollten Sie Ihre Getränkewahl genauer unter die Lupe nehmen.
- Median: Der Median zeigt Ihnen, wie Ihre Ausgaben im Vergleich zu allen anderen stehen. Vielleicht geben mehrere Personen $0 für Kaffee aus – das würde den Mittelwert niedriger machen als das, was der typische Kaffeetrinker ausgibt. In diesem Fall könnten Sie sehen, dass Sie tatsächlich weniger als der Median ausgeben, sodass Ihre Ausgaben durchaus angemessen sind.
- Modus: Der häufigste Wert. Vielleicht bestellt eine Gruppe von Freunden jeden Morgen denselben Orange Mocha Frappuccino – was ihn zur Modus-Wahl macht. Wenn Sie wissen, dass der Orange Mocha Frappuccino teuer ist, könnte das bedeuten, dass der Median auch höher ist als das, was Sie denken, dass ein typischer Kaffeetrinker bestellt.
Beispiel: Estebans Kaffeekonsum
Esteban kauft jeden Morgen einen Kaffee für $4,75. Während er glaubt, dass dies ein angemessener Preis ist, ist er neugierig, ob es typisch ist. Um ein besseres Gefühl für die durchschnittlichen Kosten zu bekommen, fragt er seine Freunde, Familie und Kollegen, wie viel sie für ihren Morgenkaffee ausgegeben haben. Das sind ihre Antworten:

| Befragter | Wie viel sie heute Morgen ausgegeben haben |
|---|---|
| 1 | $0.00 |
| 2 | $6.95 |
| 3 | $1.99 |
| 4 | $0.00 |
| 5 | $4.25 |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. Berechnung des Mittelwerts
Zuerst möchte Esteban seine erste Hypothese testen – dass er ungefähr so viel ausgibt wie alle anderen. Also würde er den Durchschnitt oder Mittelwert berechnen. Die Formel zur Berechnung des Durchschnitts lautet:
Mittelwert = Summe der Beobachtungen / Anzahl der Beobachtungen
Die Formel kann auch in der sogenannten Sigma-Notation geschrieben werden:
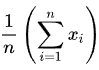
In der Sigma-Notation bedeutet das Sigma-Zeichen (Σ) “addiere”, das n-Zeichen bedeutet wie viele Beobachtungen, das x bedeutet für eine bestimmte Beobachtung, und das i bedeutet für jede Beobachtung. Das bedeutet, dass von der ersten (i = 1, unten im Sigma) bis zur letzten Beobachtung (bis n, das oben im Sigma steht) alle Werte addiert werden, und dann mit 1/n multipliziert wird. Die Sigma-Notation ist in Forschungsbereichen sehr verbreitet, da sie algebraische oder mathematische Operationen auf eine ganze Reihe von Zahlen anwendet, anstatt sie einzeln zu betrachten.
Also addieren wir alle Beobachtungen:
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
Und teilen durch 15 (Anzahl der Beobachtungen)
$78.10 / 15 = $5.21
Esteban hatte recht – er gibt weniger aus als der Mittelwert. Seine $4.75 sind günstiger als der Mittelwert von $5.21.
2. Berechnung des Medians
Um den Median zu berechnen, müssen wir die Werte von klein nach groß anordnen. Der Median ist die mittlere Zahl.
| Befragter | Wie viel sie heute Morgen ausgegeben haben |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
Der Mittelwert (Median) der Ausgaben seiner Freunde, Familie und Kollegen für Kaffee am Morgen beträgt tatsächlich $3.00, was deutlich niedriger ist als Estebans $4.75. Diese Entdeckung lässt Esteban sich weniger wohl fühlen mit seiner täglichen Kaffeegewohnheit. Er erkennt, dass er 50% mehr ausgibt als seine Kollegen, obwohl sein individueller Preis unter dem Durchschnittspreis liegt.
3. Berechnung des Modus
Zuletzt möchte Esteban sehen, was die beliebteste Wahl ist. Dafür muss er den Modus finden. Der Modus ist einfach die häufigste Beobachtung. In seinem Umfragefall haben 5 Personen $0.00 geantwortet – was dies zur häufigsten Wahl (dem Modus) macht. Obwohl dies nicht die Mehrheit der Personen ist, hat es definitiv einen großen Einfluss auf die Mittelwert- und Medianwerte. Esteban ist sich nicht ganz sicher, was er mit diesen Informationen anfangen soll – aber es gibt mehr Mathematik, die ihm helfen kann, eine Antwort zu finden!
Daten interpretieren: Schiefe, Ausreißer und Verteilungen
Esteban schaut sich die Probleme in seiner Analyse an, die aus der Verteilung seiner Antworten stammen – oder wie seine Antworten in einem Diagramm aussehen.
Schiefe
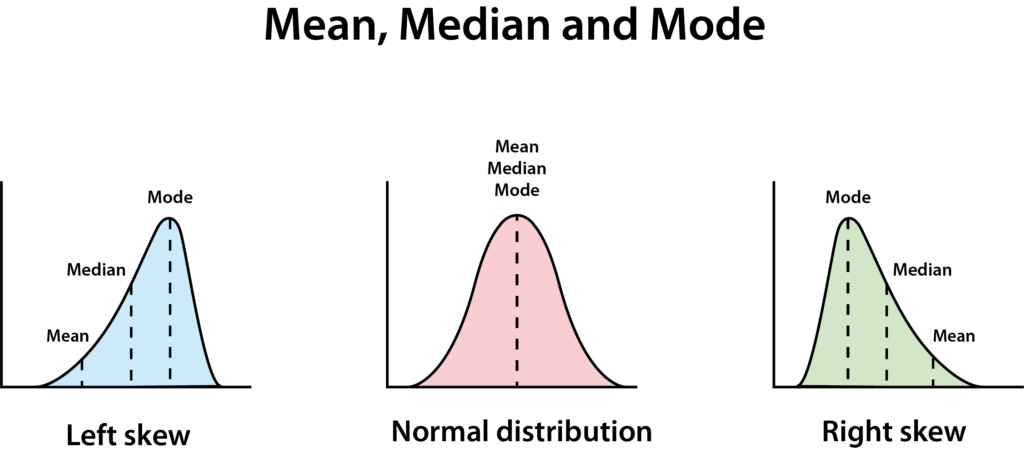
Eine normale Verteilung hat eine klare Glockenform. Eine perfekt normale Verteilung führt dazu, dass der Mittelwert, der Median und der Modus gleich sind.
Wenn sie nicht alle gleich sind, bedeutet das, dass die Daten schief sind – in diesem Fall sagen wir, dass seine Daten eine rechtsgeneigte Verteilung haben, was bedeutet, dass der Median niedriger ist als der Mittelwert. Dies geschieht oft, wenn es wenige wirklich große oder wirklich kleine Zahlen gibt, wodurch das Diagramm aussieht, als hätte es einen langen Abhang nach rechts.
Ausreißer
Als Esteban die Antworten genauer untersucht, bemerkt er einen Ausreißer: einen Kostenpunkt von 24,68 $. Dieser Wert ist deutlich höher als jeder andere. Ausreißer sind Datenpunkte, die weit von der restlichen Gruppe entfernt sind und oft von der statistischen Analyse ausgeschlossen werden, da sie die Ergebnisse verzerren können.
Bei weiterer Untersuchung erfährt Esteban, dass dieser Ausreißer die Kosten für einen Liter frisch gepressten Orangensaft darstellt, der für die gesamte Familie dieser Person an diesem Morgen gekauft wurde. Diese Ausgabe ist eindeutig nicht mit den typischen Kosten für eine einzelne Tasse Kaffee vergleichbar.
Bimodale Verteilungen
Bimodale Verteilungen treten auf, wenn man die Häufigkeitsverteilung betrachtet und nicht nur einen Gipfel sieht, sondern zwei (oder mehr). Schauen Sie sich diese Umfrageantworten an, wie viel Schüler an einem bestimmten Tag für ihr Mittagessen bezahlt haben:
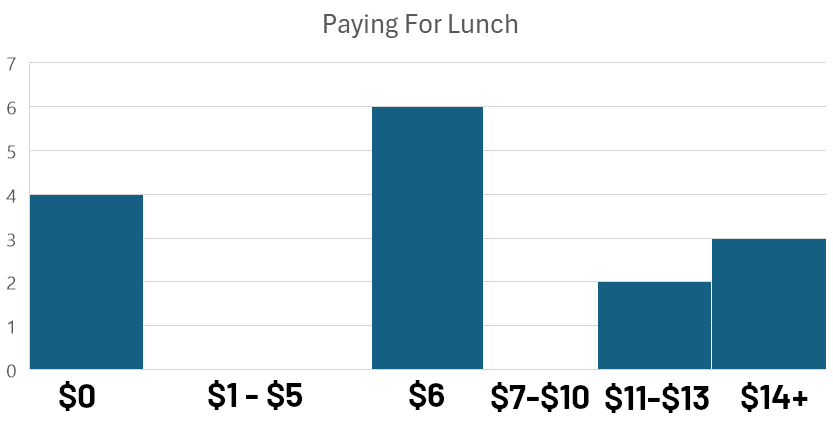
Diese Art von Diagramm, bei dem Daten in Intervalle oder ‘Bins’ für den visuellen Vergleich gruppiert werden, wird als Histogramm bezeichnet. Die Analyse, wie Beobachtungen innerhalb dieser Bins verteilt sind, wird als Häufigkeitsanalyse bezeichnet.
Beim Betrachten des Histogramms bemerken wir zwei deutliche Gipfel: einen nahe 0 $ und einen anderen nahe 6 $. Diese bimodale Verteilung (mit Modi nahe 0 $ und 6 $) deutet darauf hin, dass es zwei unterschiedliche Gruppen innerhalb der Daten gibt.
Die Identifizierung dieser Gipfel kann weitere Forschungen leiten, indem sie Fragen aufwirft wie:
- Welche Faktoren könnten diese beiden unterschiedlichen Ausgabemuster erklären?
- Was offenbaren diese Gipfel über die zugrunde liegenden Motivationen und Verhaltensweisen der Personen in diesen Gruppen?
Darüber hinaus weist die Präsenz dieser beiden Gipfel auf eine rechtsgeneigte Verteilung hin, was bedeutet, dass ein größerer Anteil der Datenpunkte am unteren Ende der Preisspanne konzentriert ist.
Bimodale Daten bedeuten nicht unbedingt, dass es zwei Antworten mit der exakt gleichen Anzahl von Beobachtungen gibt, sondern nur, dass wir zwei klare Gipfel sehen können (in diesem Fall ist 6 $ der “wahre Modus”).
Als Forscher die Daten genauer untersuchten, wurde die Erklärung offensichtlich. 0 $ waren Schüler, die ein mitgebrachtes Mittagessen von zu Hause hatten, und 6 $ waren die Kosten für das reguläre Schulmittagessen. Schüler, die mehr als 10 $ ausgaben, kauften eine Kombination von Artikeln aus dem Snackbereich der Schule und anderen Lebensmitteln, die sie auf dem Weg zur Schule kauften.

Fazit: Daten nutzen, um bessere finanzielle Entscheidungen zu treffen
Indem Sie diese drei Maße der zentralen Tendenz verstehen: Mittelwert, Median und Modus, können Sie Daten interpretieren und informiertere finanzielle Entscheidungen treffen. Egal, ob Sie Ihre Ausgaben analysieren oder größere Trends betrachten, diese Werkzeuge ermöglichen es Ihnen, bessere Geldgewohnheiten zu entwickeln. Das Sammeln und Analysieren von Ausgabedaten kann Einblicke in Ihr finanzielles Verhalten geben.
Für Schüler wie Esteban können einfache Änderungen – wie das Reduzieren von diskretionären Ausgaben – langfristige finanzielle Vorteile bringen. Wenn Esteban sieht, dass seine Ausgaben über dem Median liegen – und dass die beliebteste Wahl darin besteht, gar nichts auszugeben, hilft ihm das, den Kontext seiner Ausgabenentscheidungen und deren Bedeutung für seine Zukunft zu verstehen.