Piirangud ja logid – isikupärastatud kulutamine ja säästmine
Isikliku rahanduse suur osa keskendub pikaajalisele mõtlemisele: oma eelarve koostamine, et saaksid säästa piisavalt raha, et elada soovitud eluviisi ja mugavalt pensionile jääda.
Kuid igaühe jaoks võib “soovitud eluviis” ja “mugav pensionile jäämine” tähendada väga erinevaid asju. Päeva lõpuks teeb iga inimene iga kuu otsuse, kui palju nad kavatsevad kulutada (või tarbida) ja kui palju nad kavatsevad säästa (või investeerida).
Kui mõista selle vahetuse mõtlemisprotsessi, saad selgema ülevaate oma kulutamisest. See aitab sul tagada, et sinu tegelik kulutamine vastab sinu kavandatud kulutamisele.
Tarbimise modelleerimine – kahanevad tootlikkuse määrad
Finantsmatemaatika keskendub suuresti eksponentsiaalsele kasvule – kuidas investeering kasvab intressimäärade põhjal, kuidas säästukonto aja jooksul kasvab või kuidas luua pikaajalist rikkust. Eksponentsiaalsetel funktsioonidel on ülespoole suunatud kõver – investeeringud suurenevad aja jooksul:

Kuid kui sa kulutad selle asemel, et säästa, ei ole iga dollari eest saadud kasu sellise ülespoole suunatud kõveraga. Selle asemel ütlevad majandusteadlased, et tarbimisel on kahanevad tootlikkuse määrad.
Mõtle sellele nii – sa näed kahte korterit üürimiseks. Ühes on üks magamistuba, seadmed on 30 aastat vanad, vannituba on tilluke ja köögis pole isegi ruumi laua jaoks. See korter on hinnatud 500 dollari / kuu üüri.
Teises korteris on täiesti uued seadmed, avar vannituba eraldi vanni ja dušiga ning köögis on graniidist tööpinnad, kus on ruumi nii laua kui ka hommikusöögibaarile. See on hinnatud 1,500 dollari / kuu üüri.
Nüüd võib teine korter tõepoolest olla väärt 1,000 dollarit rohkem kuus. Kuid väärtus, mille sa saad korteri omamisest (koht, kus öösel magada, oma asjade ohutuks hoidmine, toidu valmistamine ja söömine jne), on kõige olulisem osa. Kui sa üritaksid välja selgitada kõik erinevad mugavused, mida saad kallimast korterist, et näha, kust kogu väärtus tuleb, võiks see välja näha nii:
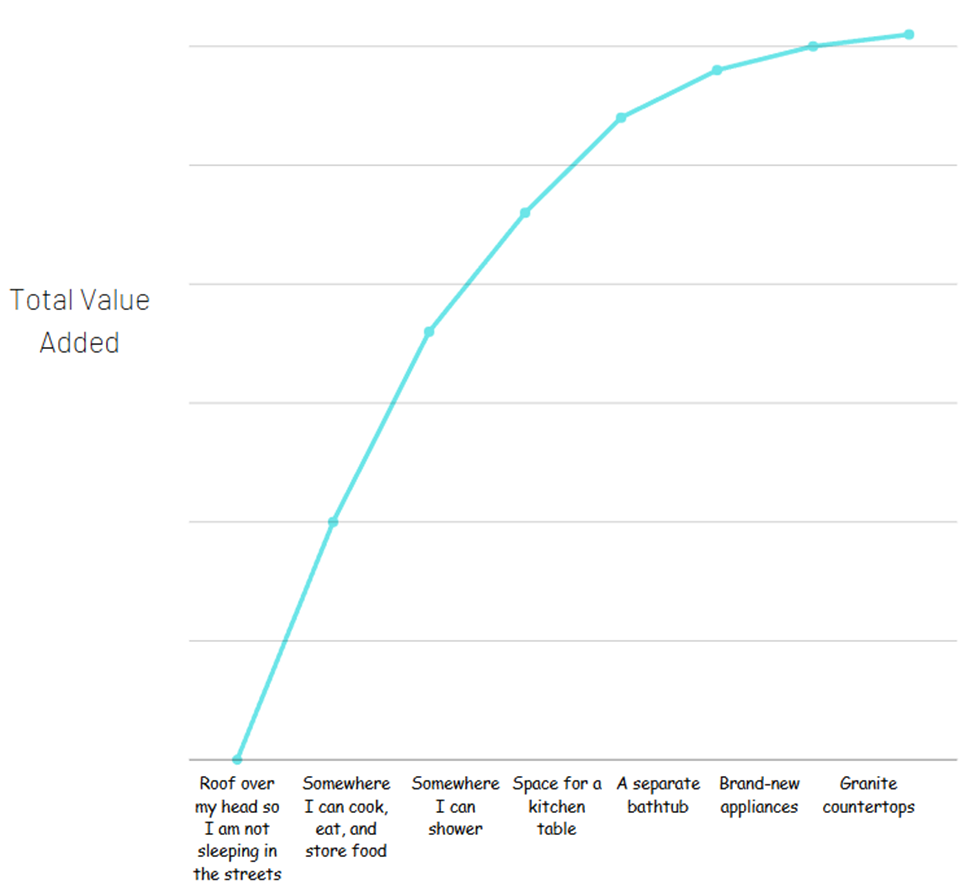
Enamik koguväärtusest tuleb põhiasjadest. See ei tähenda sugugi, et lisad ei oleks väärt – siin pole dollarimärke, vaid lihtsalt, kui palju väärtust sa saad.
Majanduses nimetatakse seda kontseptsiooni kasutuseks – rahulolu või kasu, mis tuleneb kaupade või teenuste tarbimisest. Sa märkad, et kõver tasandub, kui kulutamine suureneb. Selle matemaatiliseks modelleerimiseks kasutame logaritme, mitte eksponente.
Mis on logaritm?
Sa saad mõelda logaritmidele seoses eksponentidega samamoodi, nagu jagamine seondub korrutamisega – see on vastupidine matemaatiline funktsioon. Teisisõnu,
Kui 2^3 = 8, siis 3 on 8 logaritm alusel 2.
Majanduses ja rahanduses on logaritmid kasulikud, et näidata neid kahanevaid tootlikkuse määrasid kulutamise puhul. Näiteks, kui me tahame teha graafiku, mis näitab tarbimisega saadud kasu antud kuu jooksul, võiks graafik välja näha nii:
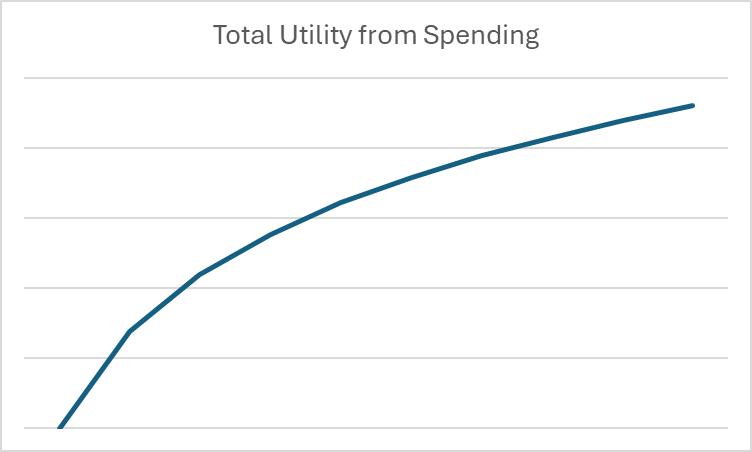
Kui me paneme oma kulutamise logaritmide ja kasu konteksti, saame hakata vaatama pikaajalisi kulutamise ja säästmise otsuseid puhtalt matemaatiliselt.
Raha ajaväärtus – diskontomäärad
Raha ajaväärtus viitab sellele, et dollar tulevikus on vähem väärt kui dollar täna. See on tingitud sellest, et nüüd ja tuleviku vahel oleksin võinud seda dollarit millegi jaoks kasutada – ja see võimalus võib olla möödas.
Kui me tahame matemaatiliselt kirjeldada raha ajaväärtust, kasutame midagi, mida nimetatakse diskontomääraks. Diskontomäär on lihtne number vahemikus 0 kuni 1, mis vastab sellele küsimusele:
Kui palju sa loobuksid täna, et saada 1 dollar 1 kuu pärast?

Igaühe diskontomäär on erinev – see viitab sellele, kui lühiajalised või pikaajalised on nende isiklikud eelistused. Nagu võid oodata, on inimesel, kellel on kõrge diskontomäär (ütleme, 0.9), palju tõenäolisem, et ta on säästja kui inimesel, kellel on madal diskontomäär (ütleme, 0.3). See on tingitud sellest, et madala diskontomääraga inimene hindab väga kõrgelt raha olemasolu just praegu – seega on nad valmis loobuma 70% selle väärtusest, et saada see kohe, mitte oodata.
Diskontomäära väljendatakse tavaliselt Kreeka tähega β. Nii et kui sinu isiklik diskontomäär on 0.95, ütleme, et β = 0.95.
Diskontomäärad ja eksponendid
Kui sa suudad tuvastada oma isikliku diskontomäära, saad seda kasutada ka selleks, et välja selgitada, kui palju sa oleksid nõus selle dollari eest võtma, kui see on veel kaugemal tulevikus kasutades eksponente.
Kui tõsta oma beta eksponendiga, mis on võrdne sellega, kui kaugel tulevikus me tahame arvutada, saame öelda, kui palju see dollar täna väärt on. Teisisõnu, β ^t = kui palju sa oleksid nõus täna võtma vahetuseks dollari eest t kuu pärast.
Meie näites, kus β = 0.95, on dollari väärtus järgmise aasta jooksul järgmine:
| Tulevased kuud | Kui palju oleksite valmis täna võtma, et ohverdada 1 dollar tulevikus |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
See tähendab, et kui teie β = 0.95, oleksite valmis võtma $0.54, et ohverdada dollar aasta pärast.
Nüüd, kui meil on mõisted logaritmidest ja diskontomääradest, saame need kokku panna, et näha, mida see tähendab pikaajaliste säästmise ja kulutamise otsuste jaoks!
Eluaegne kasu
Enamik sellest, mida te õpite isiklike rahanduse tundides, on seotud tuleviku jaoks säästmisega, eriti pensionile jäämisega. Kuid see ei ole tõeliselt teie rahaline eesmärk elus – te tõeliselt soovite maksimeerida oma kogukasu eluea jooksul. Seetõttu ei säästa keegi iga senti – te tasakaalustate oma kasu (või kasu) tänasest kulutamisest oma varanduse kasvatamisega (koos intressi võimendamisega), et saaksite seda tulevikus kulutada.
See tähendab, et iga kuu oma elus on teil selle kuu sissetulek, pluss kõik säästud, mida olete seni kogunud. Need kombineeritud ressursid on need, millega teil on võimalik töötada. Te otsustate teadlikult, kui palju neist ressurssidest te kulutate (või tarbite) ja kui palju te säästate (või investeerite). Teil on ka mingisugune arusaam intressimäärast, millega teie säästud aja jooksul kasvavad. Matemaatika mõttes valite c ja i, kus:
I + (s x (1 + r)) = c + i
Kus need muutujad viitavad:
- I = teie sissetulek sel kuul
- s = kui palju olete juba kuu alguses säästnud/investeerinud
- r = intressimäär, millega teie säästud kasvavad. Seega on teie eelmisel kuul säästud selle kuu alguseks kasvanud veidi rohkem kui eelmisel kuul.
- c = kui palju te sel kuul tarbite/kulutate
- i = kui palju te sel kuul säästate/investeerite
Tarvitamisest saadud kasu saab väljendada, võttes logaritmi teie tarbimisest:
Kasu = log(c)
Peate määrama, kui palju kulutada (ja seega säästa) igas perioodis, et maksimeerida oma kogukasu eluea jooksul, mitte ainult oma õnne praeguses hetkes. Kasutades oma diskontomäära ja eksponente, saame arvutada kasu, mida saate tarbimisest igas tuleviku perioodis, ja seejärel kõik kokku liita.
Kogukasu eluea jooksul =
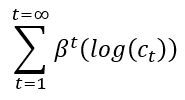
Piirid – Kasutuse ja Allahindluste Lähenemine Nullile
Esmapilgul tundub, et see võib olla lõpmatu – me liidame kokku lõpmatu arvu, seega võib see igavesti suureneda. Kuid kuna t jätkab kasvamist, tähendab see, et tulevikus rakendatav allahindlus hakkab saama ÄÄRETULT lähedaseks nullile.
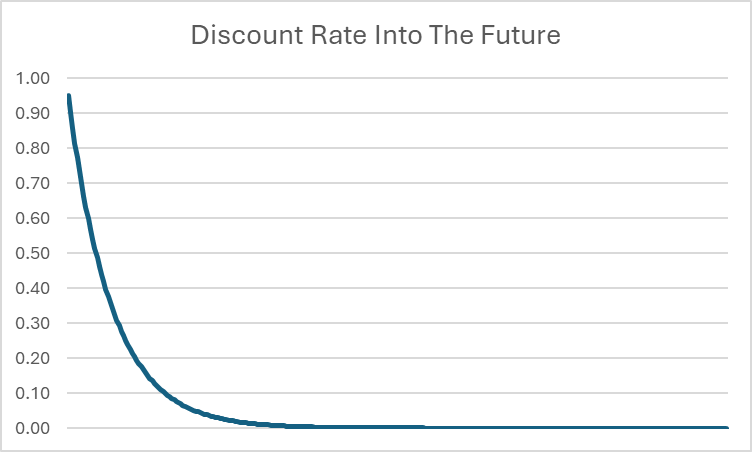
Näiteks, isegi kui β = 0.95, on 20 aasta pärast allahindluse määr langenud 0.0000045. Mida kaugemale tulevikku see läheb, seda lähemale 0-le allahindluse määr jõuab. Kuigi täpset maksimaalset eluea tarbimise summat võib olla võimatu arvutada absoluutse täpsusega (kuna see võib teoreetiliselt hõlmata lõpmatut arvu kümnendkohti), saame kindlalt öelda, et eluea jooksul on olemas tarbimise kogusummale ülemine piir.
Piire kasutatakse nende ülemiste ja alumiste piiride määratlemiseks. Saame julgelt öelda, et allahindluse määral on alumine piir 0, kuna t jätkab kasvu lõpmatusse – see läheneb pidevalt 0-le, kuid ei saavuta seda kunagi. Eluea kogukasutuse ülemine piir on samuti arvutatav (kuid selle tegemine nõuab mõningast edasijõudnud kalkulust, mis ei kuulu selle õppetunni alla).
Allahindluse Määrad ja Intressimäärad – Otsustamine Raha Säästmiseks
Kui me vaatame mööda kogu matemaatikast, näeme, et otsus kulutada või säästa põhineb tegelikult ainult kahel muutujal:
- Teie isiklik allahindluse määr (või β)
- Intressimäär r, mis määrab, kui palju teie investeeringud kasvavad
Kui on kaks inimest, kes ootavad oma säästudelt sama tootlust, kuid me märkame, et üks inimene on suur säästja ja teine suur kulutaja, saame öelda, et säästjal on kõrgem β kui kulutajal – saame kasutada tegelikku numbrit, et kvantifitseerida, KUI PALJU on keegi säästja või kulutaja.

Intressimäärade tugev mõistmine on finantskirjaoskuse jaoks ülioluline. Kui teie ainus säästmisvõimalus on madala intressimääraga säästukonto (võib-olla teenib vaid 3% aastas), on teil vähem tõenäoline, et prioriseerite pikaajalisi säästmise eesmärke. See on tingitud sellest, et te ei pruugi täielikult mõista kõrgema riski ja kõrgema tootlusega investeeringute, nagu aktsiaturg, potentsiaali.
Lõppkokkuvõttes on finantskirjaoskuse kõige olulisem aspekt olla teadlik teile kättesaadavatest investeerimisvõimalustest ja teha teadlikke otsuseid, lähtudes teie individuaalsetest oludest ja riskitaluvusest.