限制与日志 – 个性化消费与储蓄
个人理财的许多内容都集中在长期思考上:制定预算,以便能够存够钱过上自己想要的生活,并舒适地退休。
但对每个人来说,“想要的生活方式”和“舒适退休”可能意味着非常不同的事情。归根结底,每个人每个月都要做出决定,决定他们将花费(或消费)多少,以及他们将储蓄(或投资)多少。
通过理解这种权衡背后的思维过程,您可以更清晰地了解自己的消费情况。这将帮助您确保实际消费与预期消费相匹配。
消费建模 – 规模递减收益
金融数学的许多内容都集中在指数增长上 – 投资如何根据利率增长,储蓄账户如何随时间增长,或如何建立长期财富。指数函数具有向上的曲线 – 投资随着时间的推移而增大:

但当您消费而不是储蓄时,您每花费一美元所获得的收益并没有那种向上的曲线。相反,经济学家表示消费具有规模递减收益。
这样想 – 您看到两个待租公寓。一个有一间卧室,电器已经使用了30年,浴室很小,厨房甚至没有放桌子的空间。这个公寓的租金为每月500美元。
第二个公寓有全新的电器,宽敞的浴室配有独立的浴缸和淋浴,厨房有花岗岩台面,既有放桌子的空间,还有早餐吧。这个公寓的租金为每月1500美元。
现在,第二个公寓每月可能确实值多1000美元。但您拥有一个公寓(一个晚上可以睡觉的地方,安全存放您的物品,做饭和吃饭等)所获得的价值是最重要的部分。如果您试图将更昂贵的公寓所提供的所有不同设施分开,以查看所有价值来自哪里,它可能看起来像这样:
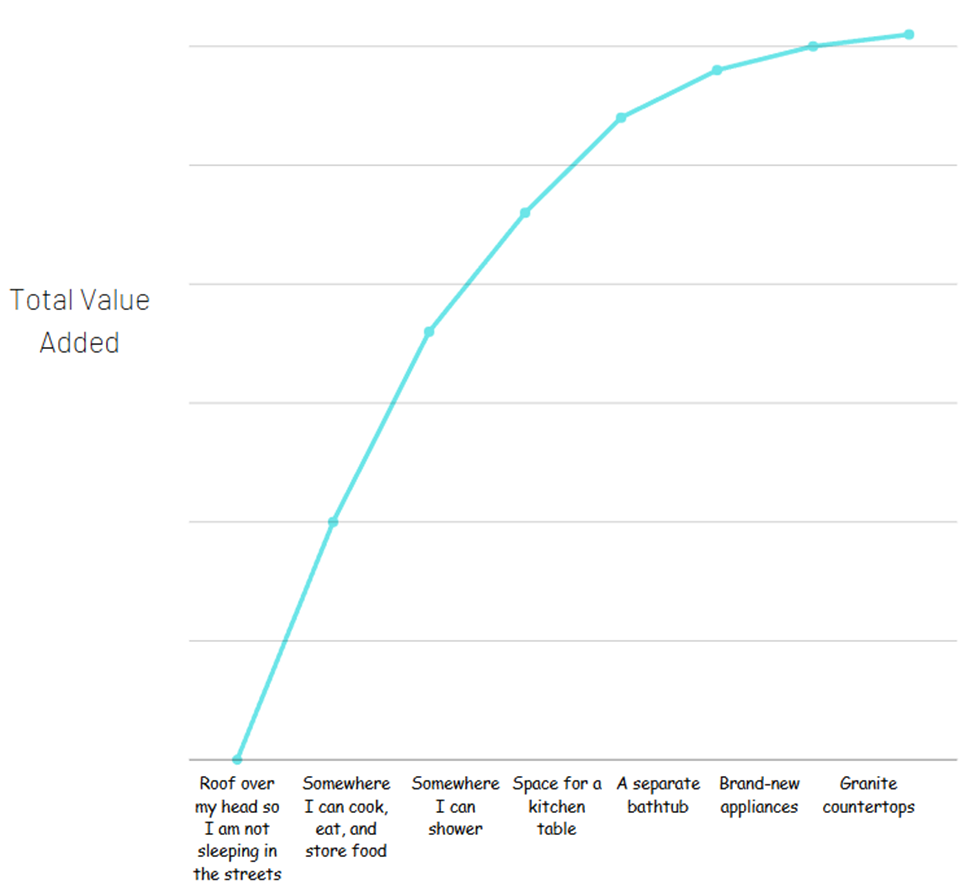
大部分总价值来自于基本的基本。这并不意味着额外的东西不值得 – 这里没有美元符号,只有您获得的价值多少。
在经济学中,这个概念被称为效用 – 从消费商品或服务中获得的满足感或利益。您会注意到,随着消费的增加,曲线变得平坦。为了在数学上建模,我们使用对数而不是指数。
什么是对数?
您可以将对数与指数的关系想象成除法与乘法的关系 – 它是相反的数学函数。换句话说,
如果2^3 = 8,那么3就是8以2为底的对数。
在经济学和金融中,对数对于显示消费的规模递减收益非常有用。例如,如果我们想制作一个图表,显示在给定月份消费所获得的效用,图表可能看起来像这样:
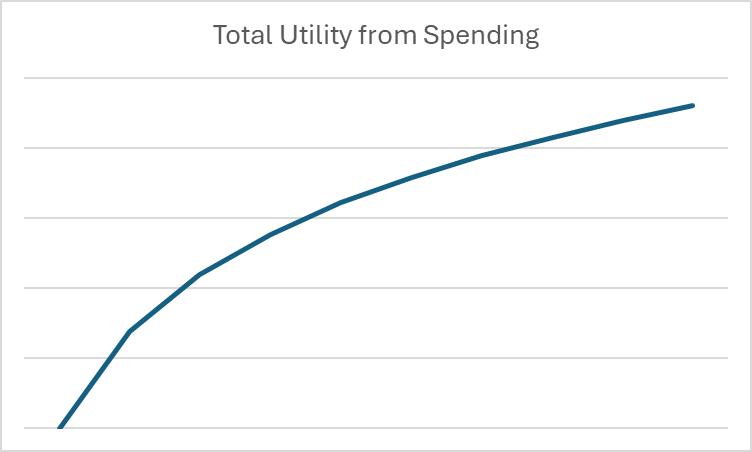
一旦我们将消费放在对数和效用的背景下,我们就可以开始纯粹从数学的角度看待长期消费和储蓄决策。
货币的时间价值 – 折现率
货币的时间价值指的是未来的一美元价值低于今天的一美元。这是因为在现在和未来之间,我可以用那一美元做某事 – 而这个机会可能已经过去。
当我们想要在数学上描述货币的时间价值时,我们使用一种叫做折现率的东西。折现率是一个介于0和1之间的简单数字,回答这个问题:
您今天愿意放弃多少才能在1个月后获得1美元?

每个人的折现率都是不同的 – 它指的是他们个人偏好的短期或长期程度。正如您可能预期的那样,折现率高的人(比如0.9)比折现率低的人(比如0.3)更有可能成为储蓄者。这是因为折现率低的人非常重视现在拥有那笔钱 – 因此他们愿意放弃70%的价值以立即获得,而不是等待。
折现率通常用希腊字母β表示。因此,如果您的个人折现率是0.95,我们会说β = 0.95。
折现率与指数
一旦您能够识别自己的个人折现率,您还可以利用它来计算如果那一美元更远在未来,您愿意接受多少通过使用指数。
通过将您的β提高到一个等于我们想要计算的未来时间的指数,我们可以说那一美元今天值多少钱。换句话说,β ^t = 您愿意今天接受多少以换取t个月后的1美元。
在我们例子中 β = 0.95,这是一美元在未来一年内的价值:
| 未来的月份 | 你愿意今天接受多少以牺牲未来的一美元 |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
这意味着如果你的 β = 0.95,你愿意接受 $0.54 来牺牲一年后的美元。
现在我们有了对数和折现率的概念,我们可以将其结合起来,看看这对长期储蓄和消费决策意味着什么!
终身效用
你在个人理财课上学到的大部分内容都是关于为未来储蓄,特别是退休。但这并不是你生活中的真正财务目标——你真正想要的是最大化你的总终身效用。这就是为什么没有人会把每一分钱都存起来——你是在平衡今天消费的收益(或效用)与通过复利增长财富以便将来消费之间的关系。
这意味着在你生活的每个月,你都有当月的收入,加上你到那时为止积累的所有储蓄。这些综合资源就是你可以使用的。你有意识地决定你将花费(或消费)多少这些资源,以及你将储蓄(或投资)多少。你也对你的储蓄将随着时间增长的利率有一定的了解。在数学上,你选择 c 和 i,其中:
I + (s x (1 + r)) = c + i
这些变量指的是:
- I = 你这个月的收入
- s = 你在这个月开始时已经储蓄/投资的金额
- r = 你的储蓄增长的利率。因此,你上个月的储蓄在这个月开始时会比你上个月多一点。
- c = 你这个月消费/支出的金额
- i = 你这个月储蓄/投资的金额
你从消费中获得的收益可以通过取消费的对数来表示:
效用 = log(c)
你需要确定在每个时期花费(因此储蓄)多少,以最大化你的总终身效用,而不仅仅是你在当下的幸福感。利用你的折现率和指数,我们可以计算你在未来任何时期消费所获得的效用,然后将它们加起来。
总终身效用 =
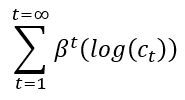
极限 – 效用和折扣接近于零
乍一看,这似乎是无限的 – 我们在加无限的数字,所以它可能会永远变得越来越大。然而,由于t不断增长,这意味着未来很远的折扣开始变得非常接近于零。
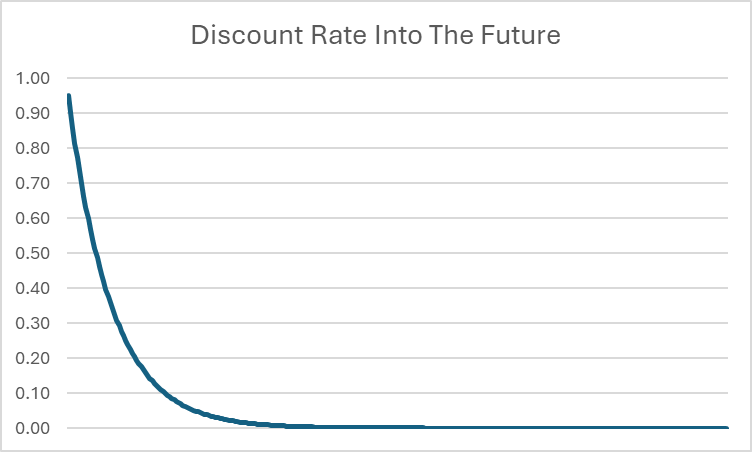
例如,即使β = 0.95,20年后的折扣率也降到了0.0000045。未来越远,折扣率越接近于0。虽然确切的终身消费最大值可能无法绝对精确地计算(因为理论上可能涉及无限的小数位),但我们可以自信地说,存在一个终身可达到的消费总量的上限。
极限用于定义这些上限和下限。我们可以安全地说,折扣率的下限是0,因为t不断增长到无限 – 它将不断接近0,但永远不会达到0。终身效用的上限也可以计算(但这样做确实需要一些高级微积分,这不在本课的范围内)。
折扣率和利率 – 选择储蓄
一旦我们超越所有的数学,我们真正看到的是,消费或储蓄的决定实际上只基于两个变量:
- 你自己的个人折扣率(或β)
- 利率r,决定你的投资将增长多少
如果有两个人对他们的储蓄预期相同的投资回报,但我们观察到一个人是大储户而另一个是大消费者,我们可以说储户的β高于消费者 – 我们可以用一个实际的数字来量化某人是多么的储蓄或消费。

对利率的强烈理解对金融素养至关重要。如果你唯一的储蓄选择是一个低利率的储蓄账户(也许每年只赚3%),你就不太可能优先考虑长期储蓄目标。这是因为你可能没有完全理解像股票市场这样的高风险、高回报投资的潜力。
最终,金融素养最重要的方面是意识到可用的投资选项,并根据你的个人情况和风险承受能力做出明智的决策。