可自由支配的开支 – 理解集中趋势
什么是可自由支配的开支?
可自由支配的开支是非必需的购买—— 想要,我们为了享受、便利或乐趣而购买的东西。例子包括娱乐、外出就餐或最新的科技小玩意。相比之下,需要是生存所必需的:食物、住房、公共事业和医疗保健。了解需求和想要之间的区别是一个关键的财务技能,尤其是在你开始管理自己的钱时。

为什么这很重要
理解需求和想要之间的区别可以帮助你做出更明智的财务选择。例如,如果你为一款新视频游戏存了钱,但你的手机坏了,你会选择哪个?手机是需求;游戏是想要。选择更换手机确保你满足必要的开支,为长期的财务安全奠定基础。
分析需求与想要:数据方法
跟踪你的开支有助于揭示你财务习惯中的模式。你可能会跟踪你和你的朋友在非必需品(如零食、娱乐或应用程序)上的花费。通过检查这些数据,你可以反思你的开支是否与优先事项一致。
事实上,研究表明,长期思考的人往往会存更多的钱,而专注于即时满足的人更可能超支。分析你的开支数据可以帮助你做出更好的财务决策,并建立更健康的金钱习惯。
使用集中趋势分析开支数据
在分析开支时,三个关键的集中趋势指标——均值、中位数和众数——有助于总结你的财务行为:
- 均值:你所有开支的平均值。虽然有用,但均值可能会受到极端值的影响(例如,有人花费远高于或低于其他人)。
- 中位数:将所有数据按顺序排列时的中间值。这可以通过避免异常值来更好地反映典型开支。
- 众数:出现频率最高的值。这可以帮助识别常见的习惯或流行的开支趋势。
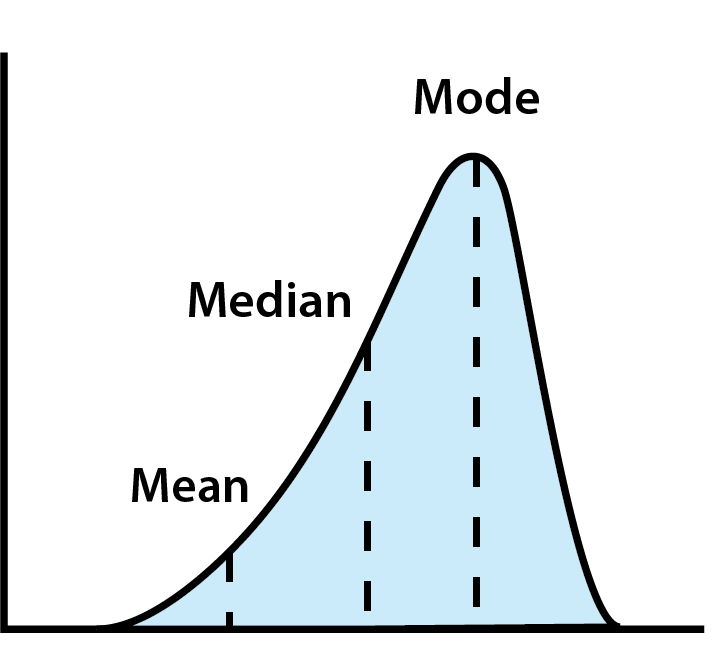
使用集中趋势分析开支数据
查看集中趋势可以帮助你更好地理解自己的预算。例如,你可能每天早上在上学或上班的路上买一杯咖啡。你意识到这可能会累积,但你认为自己的开支大致与其他人相当,因此这是一个合理的开支。
但是如果你真的问一组同龄人他们花了多少钱,这可以让你更全面地了解自己每月的实际开支。
- 均值:如果你发现自己的开支大致与平均水平相当,那么你对自己的开支习惯是正确的。但如果你发现自己花费远高于其他人,你可能需要更仔细地审视自己的饮品选择。
- 中位数:中位数告诉你你的行为与其他人相比如何。也许有几个人在咖啡上花费为$0 – 这会使均值低于典型咖啡饮用者的开支。在这种情况下,你可能会发现自己实际上花费低于中位数,因此你的开支确实是合理的。
- 众数:出现频率最高的值。也许一群朋友每天早上都一起点同样的橙色摩卡冰沙 – 使其成为众数选择。如果你知道橙色摩卡冰沙的价格较高,这可能意味着中位数也高于你认为的典型咖啡饮用者的点单。
示例:Esteban的咖啡习惯
Esteban每天早上买一杯$4.75的咖啡。虽然他认为这个价格合理,但他想知道这是否是典型的。为了更好地了解平均成本,他询问了他的朋友、家人和同事他们早上花了多少钱买咖啡。这是他们的回答:

| 受访者 | 他们今天早上花了多少钱 |
|---|---|
| 1 | $0.00 |
| 2 | $6.95 |
| 3 | $1.99 |
| 4 | $0.00 |
| 5 | $4.25 |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. 计算平均值
首先,Esteban想要验证他的第一个假设——他花费的金额大约与其他人相同。因此,他将计算平均值或均值。计算平均值的公式是:
均值 = 观察值的总和 / 观察值的数量
这个公式也可以用所谓的西格玛符号表示:
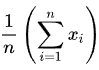
在西格玛符号中,西格玛符号(Σ)表示“加起来”,n符号表示观察的数量,x表示特定观察的值,而i表示每个观察。所以这意味着从第一个(i = 1,在西格玛的底部)到最后一个观察(到n,在西格玛的顶部),将它们的所有值相加,然后乘以1/n。西格玛符号在研究领域中非常常见,因为它显示了代数或数学运算应用于一系列数字,而不是逐个处理。
所以我们将所有观察值相加:
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
然后除以15(观察值的数量)
$78.10 / 15 = $5.21
Esteban是对的——他的花费低于均值。他的$4.75低于均值$5.21。
2. 计算中位数
要计算中位数,我们需要将数值从小到大重新排列。中位数是中间的数字。
| 受访者 | 他们今天早上花了多少钱 |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
他的朋友、家人和同事们早上喝咖啡的中间值(中位数)实际上是$3.00,显著低于Esteban的$4.75。这个发现让Esteban对他的日常咖啡习惯感到不太舒服。他意识到自己花费比同龄人多50%,尽管他的个人花费低于平均价格。
3. 计算众数
最后,Esteban想看看最受欢迎的选择是什么。为此,他需要找到众数。众数就是最常见的观察值。在他的调查中,有5个人回答$0.00——这使得它成为最常见的选择(众数)。虽然这不是大多数人的选择,但这确实对均值和中位数的选择产生了很大影响。Esteban不太确定该如何处理这些信息——但还有更多的数学可以帮助他找到答案!
解读数据:偏斜度、异常值和分布
埃斯特班正在查看他分析中来自响应分布的问题——或者说他的响应在图表上的表现。
偏斜
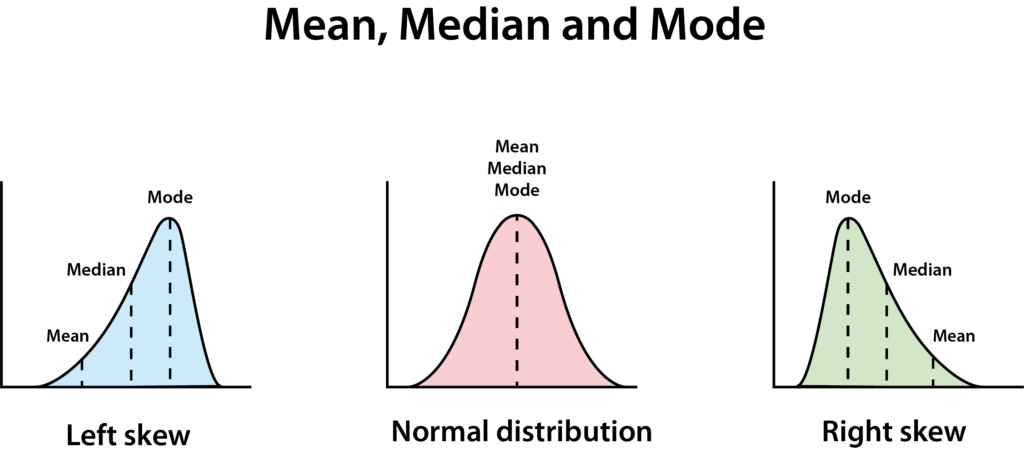
正态分布具有干净的钟形曲线。完美的正态分布意味着均值、中位数和众数都相等。
如果它们不全相等,这意味着数据是偏斜的——在这种情况下,我们说他的数据具有右偏分布,这意味着中位数低于均值。这通常发生在有少量非常大或非常小的数字时,使得图表看起来像是有一个长的滑坡向右延伸。
异常值
当埃斯特班仔细检查响应时,他注意到一个异常值:24.68美元的费用。这个值显著高于其他任何值。异常值是远离其他数据点的数据点,通常在统计分析中被排除,因为它们可能会扭曲结果。
经过进一步调查,埃斯特班了解到这个异常值代表了那个人的整个家庭在早上购买的一加仑新鲜榨橙汁的费用。这笔开支显然无法与一杯咖啡的典型费用相提并论。
双峰分布
双峰分布发生在你查看频率分布时,看到的不仅仅是一个峰,而是两个(或更多)。看看这些调查响应,了解高中生在某一天为午餐支付了多少:
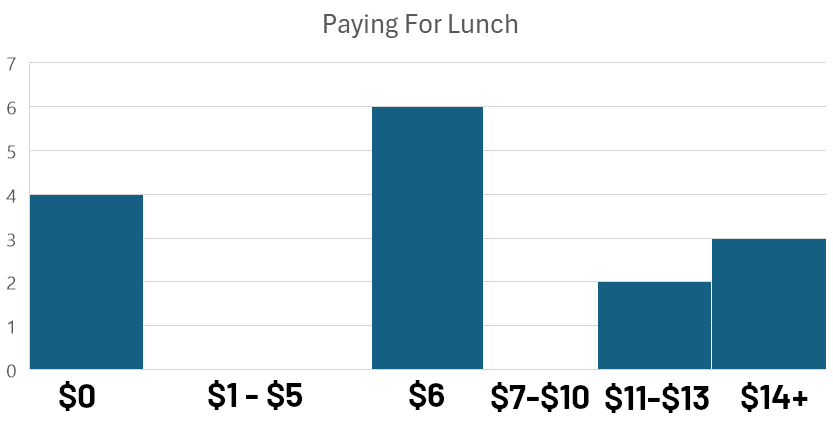
这种类型的图表,其中数据被分组为区间或“箱子”以进行视觉比较,称为直方图。在这些箱子内观察数据分布的分析称为频率分析。
观察直方图,我们注意到两个明显的峰:一个在0美元附近,另一个在6美元附近。这种双峰分布(众数在0美元和6美元附近)表明数据中存在两个不同的群体。
识别这些峰可以指导进一步的研究,提出如下问题:
- 什么因素可能解释这两种不同的消费模式?
- 这些峰揭示了这些群体中个体的潜在动机和行为的什么?
此外,这两个峰的存在表明了一种右偏分布,这意味着更大比例的数据点聚集在价格范围的较低端。
双峰数据并不一定意味着有两个响应具有完全相同的观察数量,只是我们可以看到两个明显的峰(在这种情况下,6美元是“真实众数”)。
当研究人员更仔细地查看数据时,解释变得显而易见。0美元是带午餐的学生,而6美元是常规学校午餐的费用。支付超过10美元的学生则是在学校的小吃吧购买了一些组合食品,以及他们在上学路上购买的其他食物。

结论:利用数据做出更好的财务决策
通过理解这三种集中趋势的度量:均值、中位数和众数,你可以解读数据并做出更明智的财务选择。无论你是在分析自己的消费还是观察更大的趋势,这些工具都能帮助你培养更好的理财习惯。收集和分析消费数据可以提供对你财务行为的洞察。
对于像埃斯特班这样的学生来说,简单的改变——比如减少可自由支配的消费——可以带来长期的财务利益。当埃斯特班看到他的消费高于中位数——而且最受欢迎的选择是根本不消费时,这有助于他理解自己的消费决策及其对未来的意义。