Interesse Composto
L’interesse composto è uno dei concetti più importanti nel mondo moderno ed è una pietra miliare del sistema finanziario in ogni economia. Il concetto di “interesse composto” è sorprendentemente semplice, ma incredibilmente potente!
Interesse Semplice
Prima di parlare del potere dell’interesse composto, dobbiamo prima comprendere l’interesse semplice.
Nel mondo finanziario, l’interesse semplice è il guadagno da un prestito. Ad esempio, se il tuo amico ti chiede di prestargli $100 e promette di restituirti $110 tra un anno, guadagneresti $10 prestando il denaro. L'”interesse” è il tasso di rendimento, o quanto profitto hai realizzato come percentuale dell’investimento originale. In termini di investimento, i $100 originali che hai investito sono chiamati “capitale”.

Interesse = (Restituzione – Capitale) / Capitale
Nell’esempio sopra, l’interesse guadagnato è del 10%.
(110 – 100) / 100 = 10%
Nel mondo finanziario, l’interesse è solitamente espresso come rendimento annuale. Se invece, il tuo amico promettesse di restituirti il prestito in 6 mesi, allora il “tasso di interesse annuale” verrebbe adeguato. Poiché 6 mesi sono ½ di un anno, il “tasso di interesse annuale” è il doppio del rendimento di 6 mesi.
Interesse annuale = Interesse * Durata del prestito, come percentuale di 1 anno
Quindi, se l’amico restituisce in 6 mesi, l’interesse annuale sarebbe del 20%.
Interesse annuale = 10% * 2 = 20%
Quindi, data l’opzione tra un rendimento del 20% (il tuo amico restituisce il prestito, più $10, in 6 mesi) invece di un rendimento del 10% (l’amico aspetta 12 mesi per restituire), il rendimento del 20% è chiaramente migliore.
Interesse Semplice e Obbligazioni
Investire in obbligazioni funziona con l’interesse semplice. Le obbligazioni costano tipicamente $1.000 e ognuna ha un tasso di interesse e una data di scadenza (tipicamente 30 anni dalla data di emissione).
Se compri un’obbligazione da $1.000, questa obbligazione pagherà $50 ogni anno, per 30 anni. Alla fine del 30esimo anno, riceverai l’ultimo pagamento di $50, più il tuo capitale originale di $1.000 – un semplice pagamento di interesse del 5% ogni anno.

Interesse Semplice vs Interesse Composto
L’interesse semplice è proprio questo: semplice. L’interesse composto è un po’ più complicato in superficie. Con l’interesse composto, invece di semplicemente pagare l’importo dell’interesse alla fine del prestito, l’importo da restituire viene reinvestito.
Ripensiamo al nostro esempio del nostro amico che prende in prestito $100. Quando viene a restituirci dopo 1 anno, proprio mentre ci consegna i $110, chiede di prendere in prestito quei $110 per un altro anno, e pagare lo stesso 10% di interesse. Questo significa che alla fine del prossimo anno, il suo “pagamento di interesse” sarà $110 * 10% = $11, quindi l’importo totale che restituirà sarà $121.
Poiché l’amico stava prendendo in prestito l’intero importo – compreso l’interesse del primo anno, la ricompensa è maggiore! Questo significa che ogni anno, il “rimborso” di ciascun prestito viene aggiunto all’importo originale del prestito, “compounding” il capitale (e l’interesse guadagnato) nell’anno successivo.
Esempi di Interesse Composto
L’interesse composto è comunemente usato con risparmi e investimenti. Un conto di risparmio è un esempio classico di interesse composto. La tua banca pagherà interessi sui tuoi risparmi ogni mese – e quegli interessi vengono depositati nel conto di risparmio stesso. Questo significa che il mese prossimo, guadagnerà interessi sia sul deposito originale, sia sugli interessi guadagnati nel primo mese.
Investire nel mercato azionario è anche considerato una forma di interesse composto. Se il valore di un investimento aumenta del 10% ogni anno, significa che i rendimenti di un anno precedente sono inclusi nei guadagni!
La Regola del 72
La Regola del 72 è un modo semplice per stimare quanto tempo ci vorrà affinché il tuo investimento raddoppi con l’interesse composto. Devi solo dividere 72 per il tasso di interesse annuale (in forma percentuale) – questo ti dice esattamente quanto tempo ci vorrà affinché l’investimento originale raddoppi!
| Tasso d’interesse | Tempo per raddoppiare |
|---|---|
| 1% | 72 anni |
| 2% | 36 anni |
| 5% | 14,4 anni |
| 10% | 7,2 anni |
| 20% | 3,6 anni |
Interesse composto vs semplice – In pratica
Ora abbiamo visto come funziona l’interesse semplice, con un’obbligazione, e l’interesse composto, con un conto di risparmio. Ma per vedere perché l’interesse composto è così potente, diamo un’occhiata a un confronto di 30 anni (la durata media di scadenza di un’obbligazione) per vedere la differenza nel rendimento tra i nostri due investimenti.
Interesse semplice
| Anno | Capitale | Interesse guadagnato |
| 1 | $ 1.000 | $50 |
| 2 | $ 1.000 | $50 |
| 3 | $ 1.000 | $50 |
| 4 | $ 1.000 | $50 |
| 5 | $ 1.000 | $50 |
| 6 | $ 1.000 | $50 |
| 7 | $ 1.000 | $50 |
| 8 | $ 1.000 | $50 |
| 9 | $ 1.000 | $50 |
| 10 | $ 1.000 | $50 |
| 11 | $ 1.000 | $50 |
| 12 | $ 1.000 | $50 |
| 13 | $ 1.000 | $50 |
| 14 | $ 1.000 | $50 |
| 15 | $ 1.000 | $50 |
| 16 | $ 1.000 | $50 |
| 17 | $ 1.000 | $50 |
| 18 | $ 1.000 | $50 |
| 19 | $ 1.000 | $50 |
| 20 | $ 1.000 | $50 |
| 21 | $ 1.000 | $50 |
| 22 | $ 1.000 | $50 |
| 23 | $ 1.000 | $50 |
| 24 | $ 1.000 | $50 |
| 25 | $ 1.000 | $50 |
| 26 | $ 1.000 | $50 |
| 27 | $ 1.000 | $50 |
| 28 | $ 1.000 | $50 |
| 29 | $ 1.000 | $50 |
| 30 | $ 1.000 | $50 |
| Totale | $1.500 |
Interesse Composto
| Anno | Capitale | Interesse Guadagnato |
| 1 | $ 1.000 | $ 50 |
| 2 | $ 1.050 | $ 53 |
| 3 | $ 1.103 | $ 55 |
| 4 | $ 1.158 | $ 58 |
| 5 | $ 1.216 | $ 61 |
| 6 | $ 1.276 | $ 64 |
| 7 | $ 1.340 | $ 67 |
| 8 | $ 1.407 | $ 70 |
| 9 | $ 1.477 | $ 74 |
| 10 | $ 1.551 | $ 78 |
| 11 | $ 1.629 | $ 81 |
| 12 | $ 1.710 | $ 86 |
| 13 | $ 1.796 | $ 90 |
| 14 | $ 1.886 | $ 94 |
| 15 | $ 1.980 | $ 99 |
| 16 | $ 2.079 | $ 104 |
| 17 | $ 2.183 | $ 109 |
| 18 | $ 2.292 | $ 115 |
| 19 | $ 2.407 | $ 120 |
| 20 | $ 2.527 | $ 126 |
| 21 | $ 2.653 | $ 133 |
| 22 | $ 2.786 | $ 139 |
| 23 | $ 2.925 | $ 146 |
| 24 | $ 3.072 | $ 154 |
| 25 | $ 3.225 | $ 161 |
| 26 | $ 3.386 | $ 169 |
| 27 | $ 3.556 | $ 178 |
| 28 | $ 3.733 | $ 187 |
| 29 | $ 3.920 | $ 196 |
| 30 | $ 4.116 | $ 206 |
| Totale | $3.322 |
In questo esempio, puoi vedere che l’interesse composto offre più del doppio del rendimento totale dell’interesse semplice – è potente! Se guardi un grafico del valore totale del tuo investimento, puoi anche vedere una chiara differenza di forma:
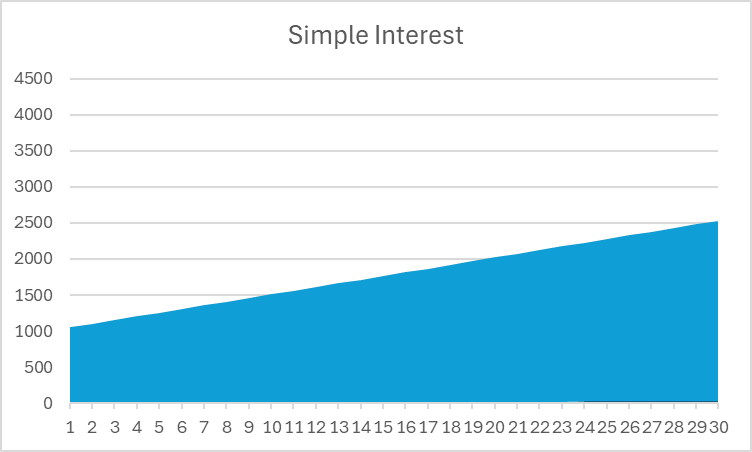
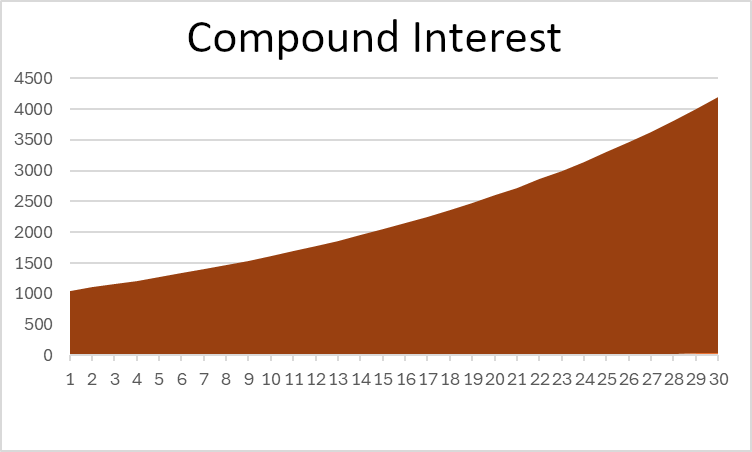
Nota che l’interesse semplice è una linea retta, mentre l’interesse composto curva verso l’alto nel tempo.
Il Caso per l’Interesse Semplice
Anche se vuoi sicuramente che i tuoi risparmi si accumulino nel tempo per ottenere un rendimento migliore a lungo termine, ciò non significa che l’interesse semplice debba essere ignorato. Significa solo che se vuoi che i risparmi si accumulino, hai un po’ più di lavoro da fare.
Prendi ad esempio l’investimento in obbligazioni. Mentre le obbligazioni pagano un interesse semplice, puoi prendere quei pagamenti e reinvestirli altrove (come depositarli in un conto di risparmio o acquistare più obbligazioni) – offrendoti “rendimenti composti” anche se ha un interesse semplice.
Finché continui a reinvestire i tuoi rendimenti (non spenderli o tenerli come contante), stai sempre accumulando!
Frequenza di Compounding
C’è un’ultima considerazione con l’interesse composto che può rendere le cose un po’ più complicate – la frequenza di accumulo.
Abbiamo accennato in precedenza che un conto di risparmio paga interessi mensilmente – anche se utilizza un tasso di interesse annuale del 5%. Questo significa che la tua banca pagherà effettivamente il 5% / 12 di interesse ogni mese (o circa lo 0,42%).
Questo significa che il tuo conto bancario si accumula a un tasso di interesse più basso, ma a una frequenza più alta, rispetto a un altro conto bancario che paga solo i suoi interessi annualmente. Poiché il tuo conto si accumula più spesso, significa che il tuo rendimento “effettivo” è un po’ più alto – con un tasso di interesse del 5% e $1.000 risparmiati, accumulare una volta darebbe $1.050, ma accumulare mensilmente termina con circa $1.051,16. Quell’extra $1,16 non è molto – ma non è nemmeno nulla.

Formula dell’Interesse Composto
Grazie al potere degli Esponenti, possiamo calcolare il saldo finale per un investimento a interesse composto senza calcolare manualmente ogni anno, come abbiamo fatto sopra. La formula è:
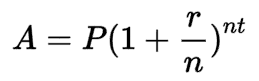
Dove:
- A è il saldo finale
- P è il capitale iniziale
- r è il tasso d’interesse (in finanza, normalmente il tasso d’interesse annuale)
- n è il numero di periodi in cui l’investimento si capitalizza
- E t è il numero di periodi di tempo che stiamo misurando.
Nel nostro esempio di capitalizzazione annuale per 30 anni, P sarebbe $1.000, r sarebbe 5%, n sarebbe 1 (una capitalizzazione all’anno), e t sarebbe 30, per 30 anni. Se stessimo calcolando l’interesse mensile, “n” sarebbe invece 12, poiché si capitalizza 12 volte all’anno.
Puoi vedere la differenza tra i diversi tipi di capitalizzazione con diversi tassi d’interesse giocando con il nostro Calcolatore di Interesse Composto!
Return To Glossary