9-08 Prezzo delle Opzioni – Modello Black-Scholes
Qualsiasi discussione sulle opzioni e sui prezzi delle opzioni sarebbe incompleta senza una menzione del Black-Scholes modello di prezzo delle opzioni.
Gli accademici Fischer Black e Myron Scholes, in un articolo che hanno scritto nel 1973, hanno dichiarato la loro teoria secondo cui un’opzione era implicita nel prezzo di qualsiasi titolo negoziato.
Riferendosi al lavoro di alcuni dei più famosi economisti, come Paul Samuelson, Black e Scholes hanno sviluppato non una, ma tre “posizioni” per la tua considerazione.
- Il Modello Black-Scholes: Un calcolo matematico riguardante le azioni (stocks).
- La PDE (Equazione Differenziale Parziale) di Black-Scholes: Questa traccia il movimento di un certo titolo.
- La Formula di Black-Scholes: Questa cerca di calcolare i prezzi per le opzioni put e opzioni call .
Se non sei un matematico dedicato e senza speranza, devi solo sapere come il lavoro di Black-Scholes potrebbe influenzare le tue attività di investimento. Mentre molti esperti dichiarano i limiti di questa teoria, potresti adottare le previsioni e le proiezioni offerte dai calcoli di Black-Scholes per aiutare la tua attività di opzioni.
La formula di Black-Scholes è utilizzata per ottenere il prezzo delle opzioni put e call europee. Viene ottenuta risolvendo la PDE di Black-Scholes – vedi derivazione qui sotto.
Utilizzando questa formula, il valore di un’opzione call in termini dei parametri di Black-Scholes è:
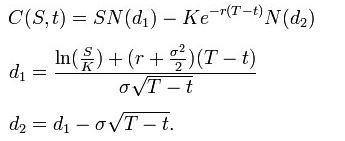
Il prezzo di un opzioni put è:
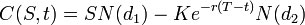
Per entrambi, come sopra:
- N(•) è la funzione di distribuzione cumulativa della distribuzione normale standard
- T – t è il tempo fino alla scadenza
- S è il prezzo spot dell’asset sottostante
- K è il prezzo di esercizio
- r è il tasso privo di rischio (tasso annuale, espresso in termini di capitalizzazione continua)
- σ è la volatilità nei log-ritorni dell’underlying

