Límites y Registros – Gastos y Ahorros Personalizados
Gran parte de las finanzas personales se centra en el pensamiento a largo plazo: construir tu presupuesto para que puedas ahorrar suficiente dinero para vivir el estilo de vida que deseas y retirarte cómodamente.
Pero para cada persona individual, “un estilo de vida que deseas” y “retirarte cómodamente” pueden significar cosas muy diferentes. Al final del día, cada persona toma una decisión cada mes en la que trabaja sobre cuánto va a gastar (o consumir) y cuánto va a ahorrar (o invertir).
Al comprender el proceso de pensamiento detrás de este intercambio, puedes obtener una imagen más clara de tus propios gastos. Esto te ayudará a asegurar que tus gastos reales coincidan con tus gastos previstos.
Modelando el Consumo – Rendimientos Decrecientes a Escala
Gran parte de las matemáticas financieras se centra en el crecimiento exponencial: cómo crece una inversión en función de una tasa de interés, cómo crece una cuenta de ahorros con el tiempo, o cómo construir riqueza a largo plazo. Las funciones exponenciales tienen una curva ascendente: las inversiones crecen con el tiempo:

Pero cuando gastas en lugar de ahorrar, el beneficio que obtienes por cada dólar que gastas no tiene esa curva ascendente. En cambio, los economistas dicen que el consumo tiene rendimientos decrecientes a escala.
Piénsalo de esta manera: ves dos apartamentos en alquiler. Uno tiene una habitación, los electrodomésticos tienen 30 años, el baño es pequeño y la cocina ni siquiera tiene espacio para una mesa. Este apartamento está listado por $500 / mes de alquiler.
El segundo apartamento tiene electrodomésticos nuevos, un baño espacioso con bañera y ducha separadas, y la cocina tiene encimeras de granito con espacio tanto para una mesa como para una barra de desayuno. Este está listado por $1,500 / mes de alquiler.
Ahora, el segundo apartamento puede valer muy bien $1,000 más por mes. Pero el valor que recibes por tener un apartamento (un lugar para dormir por la noche, almacenar tus pertenencias de forma segura, cocinar y comer, etc.) es la parte más importante. Si intentaras desglosar todas las diferentes comodidades que obtienes con el apartamento más caro para ver de dónde proviene todo el valor, podría verse así:
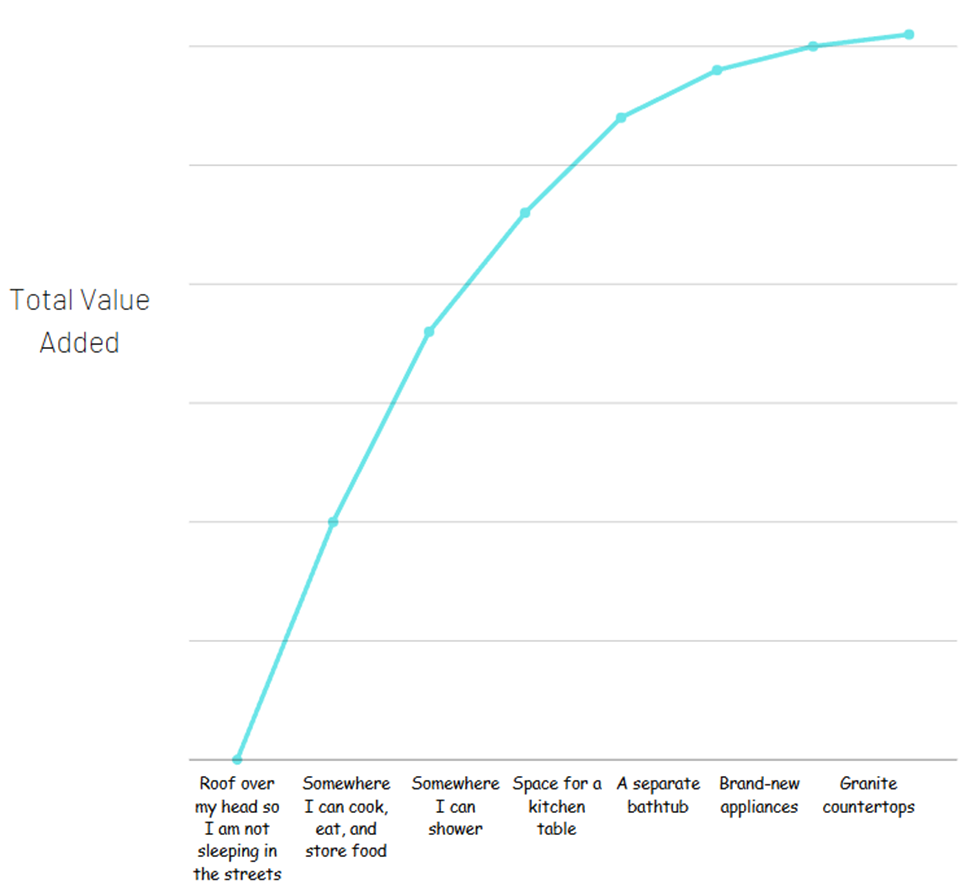
La mayor parte del valor total proviene de lo básico de lo básico. Eso de ninguna manera significa que los extras no valgan la pena: aquí no hay signos de dólar, solo cuánto valor estás obteniendo.
En economía, este concepto se llama utilidad: la satisfacción o beneficio derivado del consumo de bienes o servicios. Notarás que la curva se aplana a medida que aumentan los gastos. Para modelar esto matemáticamente, usamos logaritmos en lugar de exponentes.
¿Qué es un Logaritmo?
Puedes pensar en los logaritmos en relación con los exponentes de la misma manera que la división se relaciona con la multiplicación: es la función matemática opuesta. En otras palabras,
Si 2^3 = 8, entonces 3 es el logaritmo de 8 en base 2.
En economía y finanzas, los logaritmos son útiles para mostrar estos rendimientos decrecientes a escala para el gasto. Por ejemplo, si queremos hacer un gráfico que muestre la utilidad recibida por el consumo durante un mes determinado, el gráfico podría verse así:
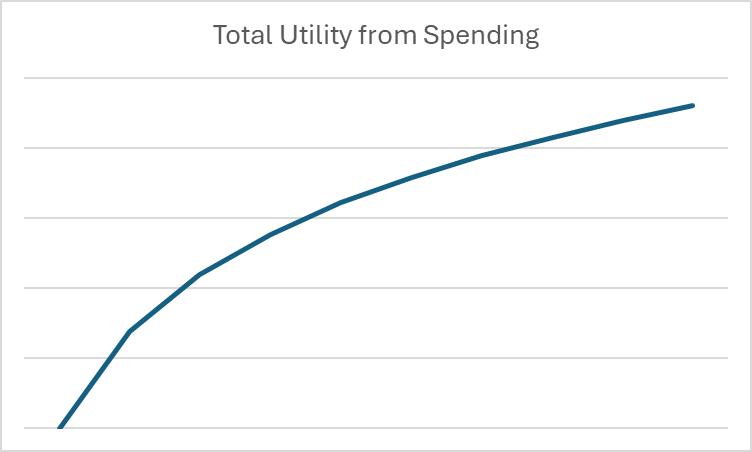
Una vez que ponemos nuestros gastos en el contexto de los logaritmos y la utilidad, podemos comenzar a ver decisiones de gasto y ahorro a largo plazo puramente en matemáticas.
Valor Temporal del Dinero – Tasas de Descuento
El Valor Temporal del Dinero se refiere al hecho de que un dólar en el futuro vale menos que un dólar hoy. Esto se debe a que entre ahora y el futuro, podría haber usado ese dólar para hacer algo, y esa oportunidad podría haber pasado.
Cuando queremos describir matemáticamente el Valor Temporal del Dinero, usamos algo llamado tasa de descuento. La tasa de descuento es un número simple entre 0 y 1 que responde a esta pregunta:
¿Cuánto estarías dispuesto a renunciar hoy para obtener $1 en 1 mes?

La tasa de descuento de cada persona es diferente: se refiere a cuán a corto o largo plazo son sus preferencias personales. Como puedes esperar, una persona con una alta tasa de descuento (digamos, 0.9) es mucho más probable que sea ahorradora que alguien con una baja tasa de descuento (digamos, 0.3). Eso se debe a que una persona con una baja tasa de descuento valora mucho tener ese dinero ahora mismo, por lo que está dispuesta a renunciar al 70% de su valor para obtenerlo de inmediato en lugar de esperar.
La tasa de descuento generalmente se expresa con la letra griega β. Así que si tu tasa de descuento personal es 0.95, diríamos β = 0.95.
Tasas de Descuento y Exponentes
Una vez que puedes identificar tu propia tasa de descuento personal, también puedes usar eso para averiguar cuánto aceptarías por ese dólar si está aún más lejos en el futuro usando exponentes.
Al elevar tu beta por un exponente igual a cuán lejos en el futuro queremos calcular, podemos decir cuánto vale ese dólar hoy. En otras palabras, β ^t = cuánto estarías dispuesto a aceptar hoy a cambio de un dólar t meses a partir de ahora.
En nuestro ejemplo de β = 0.95, esto es lo que vale un dólar durante el próximo año:
| Meses en el Futuro | Cuánto estarías dispuesto a aceptar hoy para sacrificar $1 en el futuro |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
Esto significa que si tu β = 0.95, estarías dispuesto a aceptar $0.54 para sacrificar un dólar dentro de un año.
Ahora que tenemos el concepto de logaritmos y tasas de descuento, podemos unirlo para ver qué significa para las decisiones de ahorro y gasto a largo plazo.
Utilidad de por Vida
La mayor parte de lo que aprendes en una clase de finanzas personales se trata de ahorrar para el futuro, particularmente para la jubilación. Pero ese no es realmente tu objetivo financiero en la vida: realmente quieres maximizar tu utilidad total de por vida. Por eso nadie ahorra cada centavo: estás equilibrando tu beneficio (o utilidad) de gastar hoy contra el crecimiento de tu riqueza (a través del poder del interés compuesto) para que puedas gastarlo en el futuro.
Esto significa que cada mes de tu vida, tienes tu ingreso de ese mes, más todos los ahorros que has acumulado hasta entonces. Estos recursos combinados son con los que tienes que trabajar. Decides conscientemente cuánto de estos recursos gastarás (o consumirás) y cuánto ahorrarás (o invertirás). También tienes cierta comprensión de la tasa de interés a la que crecerán tus ahorros con el tiempo. En términos matemáticos, estás eligiendo c y i donde:
I + (s x (1 + r)) = c + i
Donde estas variables se refieren a:
- I = tu ingreso este mes
- s = cuánto ya has ahorrado/invertido al inicio del mes
- r = la tasa de interés a la que están creciendo tus ahorros. Así que tus ahorros del mes pasado habrán crecido un poco más al inicio de este mes que lo que tenías el mes pasado.
- c = cuánto consumes/gastas este mes
- i = cuánto ahorras/inviertes este mes
El beneficio que obtienes del consumo se puede expresar tomando el logaritmo de tu consumo:
Utilidad = log(c)
Necesitas determinar cuánto gastar (y, en consecuencia, ahorrar) en cada período para maximizar tu utilidad total de por vida, no solo tu felicidad en el momento presente. Usando tu tasa de descuento y exponentes, podemos calcular la utilidad que obtendrás del consumo en cualquier período en el futuro, y luego sumarlos todos.
Utilidad Total de por Vida =
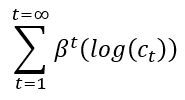
Límites – Enfoques de Utilidad y Descuentos Acercándose a Cero
Al principio, parece que esto podría ser infinito: estamos sumando números infinitos, por lo que podría seguir creciendo para siempre. Sin embargo, dado que t sigue creciendo, significa que el descuento aplicado en un futuro lejano comienza a acercarse MUCHO a cero.
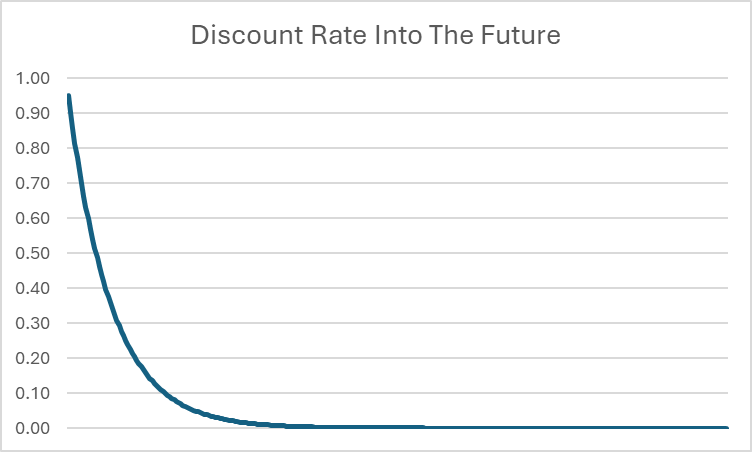
Por ejemplo, incluso si β = 0.95, la tasa de descuento en 20 años baja hasta 0.0000045. Cuanto más lejos en el futuro va, más cerca de 0 se vuelve la tasa de descuento. Si bien la cantidad máxima exacta de consumo a lo largo de la vida puede ser imposible de calcular con precisión absoluta (ya que podría involucrar teóricamente un número infinito de decimales), podemos afirmar con confianza que existe un límite superior a la cantidad total de consumo alcanzable a lo largo de una vida.
Los límites se utilizan para definir esos límites superiores e inferiores. Podemos decir con seguridad que la tasa de descuento tiene un límite inferior de 0 a medida que t sigue creciendo hacia el infinito: seguirá acercándose a 0, pero nunca lo alcanzará. El límite superior de la utilidad total a lo largo de la vida también se puede calcular (pero hacerlo requiere un cálculo avanzado, que no es parte de esta lección).
Tasas de Descuento y Tasas de Interés – Elegir Ahorrar
Una vez que miramos más allá de toda la matemática, lo que realmente podemos ver es que la decisión de gastar o ahorrar se basa realmente en solo dos variables:
- Tu propia tasa de descuento personal (o β)
- La tasa de interés r, que determina cuánto crecerán tus inversiones
Si hay dos personas que esperan el mismo retorno de inversión por sus ahorros, pero observamos que una persona es un gran ahorrador y la otra un gran gastador, podemos decir que el ahorrador tiene un β más alto que el gastador: podemos usar un número real para cuantificar CUÁNTO ahorrador o gastador es alguien.

Una comprensión sólida de las tasas de interés es crucial para la alfabetización financiera. Si tu única opción de ahorro es una cuenta de ahorros de bajo interés (quizás ganando solo un 3% anualmente), es menos probable que priorices los objetivos de ahorro a largo plazo. Esto se debe a que podrías no comprender completamente el potencial de inversiones de mayor riesgo y mayor recompensa, como el mercado de valores.
En última instancia, el aspecto más importante de la alfabetización financiera es ser consciente de las opciones de inversión disponibles para ti y tomar decisiones informadas basadas en tus circunstancias individuales y tolerancia al riesgo.