Gastos Discrecionales – Entendiendo la Tendencia Central
¿Qué Son los Gastos Discrecionales?
Los gastos discrecionales son compras no esenciales— deseos, cosas que compramos por placer, conveniencia o diversión. Ejemplos incluyen entretenimiento, salir a cenar o los últimos gadgets tecnológicos. En contraste, necesidades son esenciales para la supervivencia: comida, vivienda, servicios públicos y atención médica. Conocer la diferencia entre necesidades y deseos es una habilidad financiera clave, especialmente cuando comienzas a manejar tu propio dinero.

Por Qué Es Importante
Entender la diferencia entre necesidades y deseos te ayuda a tomar decisiones financieras más inteligentes. Por ejemplo, si has ahorrado para un nuevo videojuego pero tu teléfono se rompe, ¿cuál eliges? El teléfono es una necesidad; el juego es un deseo. Elegir reemplazar el teléfono asegura que cubras un gasto necesario, preparándote para la seguridad financiera a largo plazo.
Analizando Necesidades vs. Deseos: Un Enfoque de Datos
Rastrear tus gastos ayuda a revelar patrones en tus hábitos financieros. Podrías rastrear cuánto gastas tú y tus amigos en artículos no esenciales como bocadillos, entretenimiento o aplicaciones. Al examinar estos datos, puedes reflexionar sobre si tus gastos se alinean con tus prioridades.
De hecho, investigaciones muestran que las personas que piensan a largo plazo tienden a ahorrar más, mientras que aquellas enfocadas en la gratificación inmediata son más propensas a gastar de más. Analizar tus datos de gasto puede ayudarte a tomar mejores decisiones financieras y construir hábitos de dinero más saludables.
Usando la Tendencia Central para Analizar Datos de Gasto
Al analizar el gasto, tres medidas clave de tendencia central—media, mediana y moda—ayudan a resumir tu comportamiento financiero:
- Media: El promedio de todos tus gastos. Aunque es útil, la media puede estar sesgada por valores extremos (como alguien que gasta mucho más o menos que los demás).
- Mediana: El valor medio cuando todos los datos están ordenados. Esto da una mejor idea del gasto típico al evitar valores atípicos.
- Moda: El valor más frecuente. Esto puede ayudar a identificar hábitos comunes o tendencias populares en el gasto.
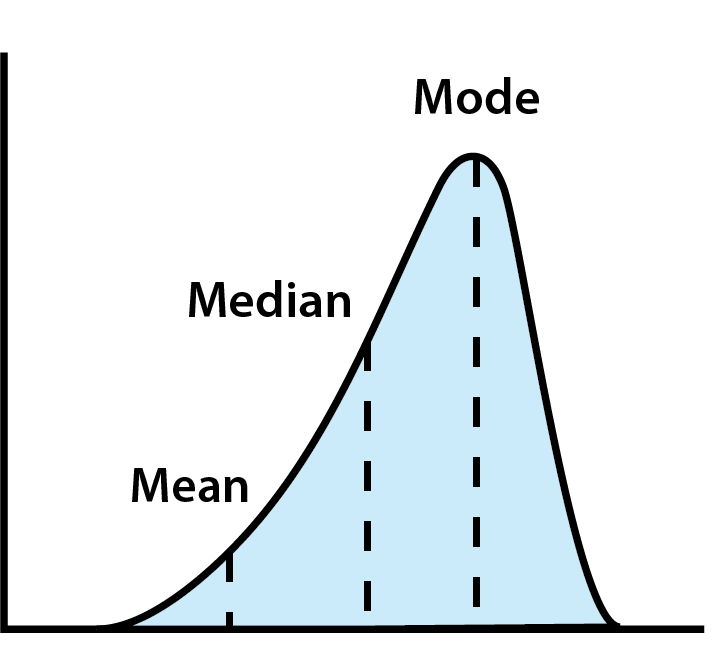
Usando la Tendencia Central para Analizar Datos de Gasto
Mirar la tendencia central puede ayudar a poner tu propio presupuesto en perspectiva. Por ejemplo, podrías comprar un café cada mañana de camino a la escuela o al trabajo. Te das cuenta de que esto puede acumularse, pero piensas que estás gastando aproximadamente lo mismo que la siguiente persona (o chica), así que es un gasto razonable.
Pero si realmente preguntas a un grupo de tus compañeros cuánto gastan, puede darte una perspectiva más amplia de cuánto estás gastando realmente cada mes.
- Media: Si descubres que estás gastando aproximadamente lo mismo que el promedio, entonces tenías razón sobre tus propios hábitos de gasto. Pero si descubres que estás gastando mucho más que los demás, podrías mirar más de cerca tus elecciones de bebida.
- Mediana: La mediana te dice cómo se ajustan tus acciones con las de los demás. Tal vez varias personas gastan $0 en café; eso sesgaría la media más baja de lo que gasta un bebedor de café típico. En este caso, podrías ver que en realidad gastas menos que la mediana, así que tu gasto es razonable.
- Moda: El valor más frecuente. Tal vez un grupo de amigos está pidiendo el mismo Orange Mocha Frappuccino juntos cada mañana, convirtiéndolo en la elección de moda. Si sabes que el Orange Mocha Frappuccino es caro, podría significar que la mediana también está sesgada más alta de lo que piensas que un bebedor de café típico está pidiendo.
Ejemplo: El Hábito de Café de Esteban
Esteban compra un café de $4.75 cada mañana. Aunque cree que este es un precio razonable, tiene curiosidad por saber si es típico. Para tener una mejor idea del costo promedio, pregunta a sus amigos, familiares y compañeros de trabajo cuánto gastaron en su café de la mañana. Estas son sus respuestas:

| Respondente | Cuánto Gastaron Esta Mañana |
|---|---|
| 1 | $0.00 |
| 2 | $6.95 |
| 3 | $1.99 |
| 4 | $0.00 |
| 5 | $4.25 |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. Cálculo de la Media
Primero, Esteban quiere probar su primera hipótesis: que está gastando aproximadamente el promedio de todos los demás. Así que calcularía el promedio, o media. La fórmula para calcular el promedio es:
Media = suma de observaciones / conteo de observaciones
La fórmula también se puede escribir en lo que se llama Notación Sigma:
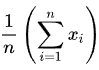
Con la Notación Sigma, el signo Sigma (Σ) significa “sumar”, el signo n significa cuántas observaciones, el x significa para una observación específica, y el i significa para cada observación. Así que lo que esto dice es que desde la primera (i = 1, en la parte inferior del sigma) hasta la última observación (hasta n, que está en la parte superior del sigma), suma todos sus valores, luego multiplica por 1/n. La Notación Sigma es muy común en campos de investigación, ya que muestra operaciones algebraicas o matemáticas aplicadas a una serie completa de números, en lugar de uno a la vez.
Así que sumamos todas las observaciones:
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
Y divide por 15 (conteo de observaciones)
$78.10 / 15 = $5.21
Esteban tenía razón: está gastando menos que la media. Su $4.75 es más barato que el valor medio de $5.21.
2. Cálculo de la Mediana
Para calcular la mediana, necesitamos reorganizar los órdenes de menor a mayor. La mediana es el número del medio.
| Respondente | Cuánto Gastaron Esta Mañana |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
El valor medio (mediana) de los gastos de café por la mañana de sus amigos, familiares y compañeros de trabajo es en realidad $3.00, significativamente más bajo que el $4.75 de Esteban. Este descubrimiento hace que Esteban se sienta menos cómodo con su hábito diario de café. Se da cuenta de que está gastando un 50% más que sus compañeros, a pesar de que su costo individual está por debajo del precio promedio.
3. Cálculo de la Moda
Por último, Esteban quiere ver cuál es la opción más popular. Para esto, necesita encontrar la moda. La moda es simplemente la observación más común. En el caso de su encuesta, 5 personas respondieron $0.00, lo que convierte esto en la opción más común (la moda). Aunque no es la mayoría de las personas, esto definitivamente tiene un gran impacto en las elecciones de media y mediana. Esteban no está muy seguro de qué hacer con esta información, ¡pero hay más matemáticas para ayudarlo a encontrar una respuesta!
Interpretando los Datos: Asimetría, Valores Atípicos y Distribuciones
Esteban está mirando los problemas en su análisis que provienen de la distribución de sus respuestas – o cómo se ven sus respuestas en un gráfico.
Sesgo
Una distribución normal tiene una forma de campana limpia. Una distribución perfectamente normal resulta en que la media, la mediana y la moda son todas iguales.
Si no son todas iguales, significa que los datos están sesgados – en este caso, decimos que sus datos tienen una distribución sesgada a la derecha, lo que significa que la mediana es menor que la media. Esto a menudo sucede cuando hay pocos números realmente grandes o realmente pequeños, haciendo que el gráfico parezca tener una larga pendiente hacia la derecha.
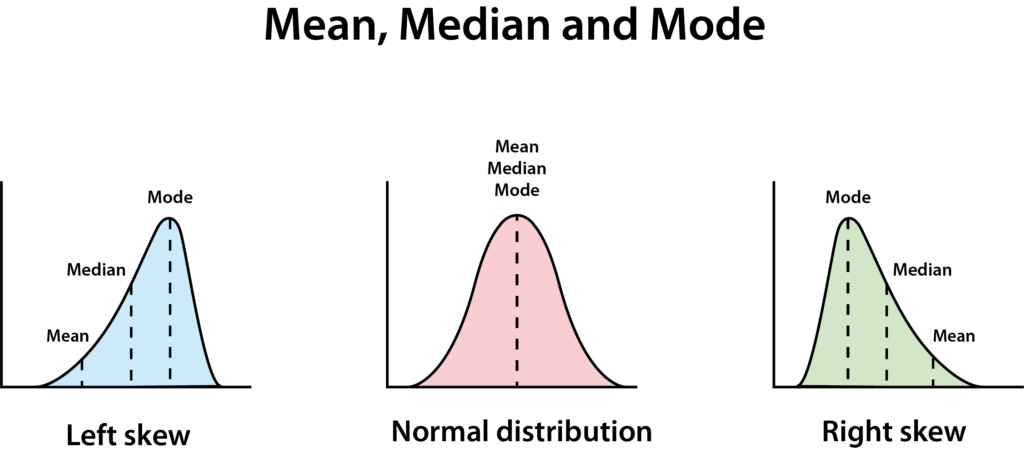
Valores atípicos
Cuando Esteban examina las respuestas de cerca, nota un valor atípico: un costo de $24.68. Este valor es significativamente más alto que cualquier otro. Los valores atípicos son puntos de datos que están muy alejados del resto del grupo y a menudo se excluyen del análisis estadístico porque pueden sesgar los resultados.
Tras una investigación más profunda, Esteban aprende que este valor atípico representa el costo de un galón de jugo de naranja recién exprimido comprado para toda la familia de esa persona esa mañana. Este gasto claramente no es comparable al costo típico de una sola taza de café.
Distribuciones bimodales
Las distribuciones bimodales ocurren cuando miras la distribución de frecuencias y no ves solo un pico, sino dos (o más). Echa un vistazo a estas respuestas de la encuesta sobre cuánto pagaron los estudiantes de secundaria por sus almuerzos en un día determinado:
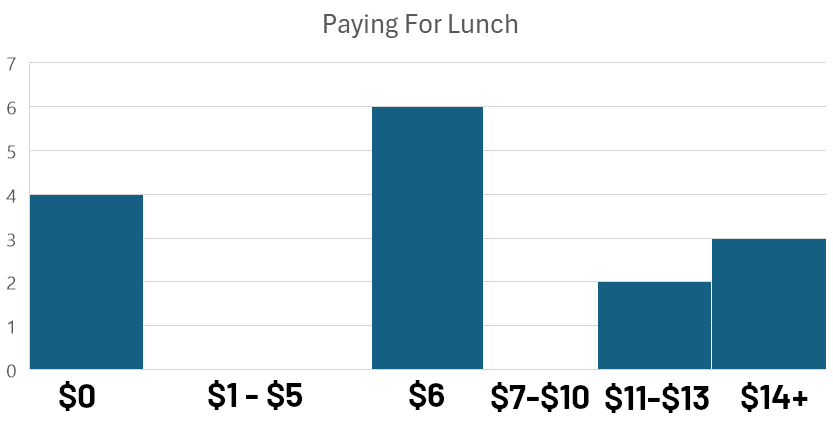
Este tipo de gráfico, donde los datos se agrupan en intervalos o ‘bins’ para comparación visual, se llama histograma. El análisis de cómo se distribuyen las observaciones dentro de estos bins se conoce como análisis de frecuencia.
Al observar el histograma, notamos dos picos distintos: uno cerca de $0 y otro cerca de $6. Esta distribución bimodal (con modos cerca de $0 y $6) sugiere que hay dos grupos distintos dentro de los datos.
Identificar estos picos puede guiar investigaciones adicionales al plantear preguntas como:
- ¿Qué factores podrían explicar estos dos patrones de gasto distintos?
- ¿Qué revelan estos picos sobre las motivaciones y comportamientos subyacentes de los individuos en estos grupos?
Además, la presencia de estos dos picos indica una distribución sesgada a la derecha, lo que significa que una mayor proporción de los puntos de datos están agrupados hacia el extremo inferior del rango de precios.
Los datos bimodales no significan necesariamente que haya dos respuestas con el mismo número exacto de observaciones, solo que podemos ver dos picos claros (en este caso, $6 es la “Moda Verdadera”).
Cuando los investigadores miraron más de cerca los datos, la explicación se volvió obvia. $0 eran estudiantes que trajeron un almuerzo empacado de casa y $6 era el costo del almuerzo escolar regular. Los estudiantes que pagaron más de $10 estaban comprando una combinación de artículos de la cafetería de la escuela y otros alimentos que compraron en el camino a la escuela.

Conclusión: Usando datos para tomar mejores decisiones financieras
Al comprender estas tres medidas de tendencia central: media, mediana y moda, puedes interpretar datos y tomar decisiones financieras más informadas. Ya sea que estés analizando tus gastos o mirando tendencias más grandes, estas herramientas te empoderan para desarrollar mejores hábitos de dinero. Recopilar y analizar datos de gastos puede proporcionar información sobre tu comportamiento financiero.
Para estudiantes como Esteban, cambios simples—como reducir las compras discrecionales—pueden llevar a beneficios financieros a largo plazo. Cuando Esteban ve que sus gastos están por encima de la mediana – y que la opción más popular es no gastar en absoluto, ayuda a poner en contexto sus decisiones de gasto y lo que eso significa para su futuro.