Despesas Discricionárias – Compreendendo a Tendência Central
O Que São Despesas Discricionárias?
Despesas discricionárias são compras não essenciais— desejos, coisas que compramos para prazer, conveniência ou diversão. Exemplos incluem entretenimento, refeições fora de casa ou os últimos gadgets tecnológicos. Em contraste, necessidades são essenciais para a sobrevivência: comida, moradia, utilidades e saúde. Conhecer a diferença entre necessidades e desejos é uma habilidade financeira chave, especialmente quando você começa a gerenciar seu próprio dinheiro.

Por Que Isso Importa
Compreender a diferença entre necessidades e desejos ajuda você a tomar decisões financeiras mais inteligentes. Por exemplo, se você economizou para um novo videogame, mas seu telefone quebra, qual você escolhe? O telefone é uma necessidade; o jogo é um desejo. Optar por substituir o telefone garante que você atenda a uma despesa necessária, preparando-o para a segurança financeira a longo prazo.
Analisando Necessidades vs. Desejos: Uma Abordagem de Dados
Rastrear seus gastos ajuda a revelar padrões em seus hábitos financeiros. Você pode rastrear quanto você e seus amigos gastam em itens não essenciais, como lanches, entretenimento ou aplicativos. Ao examinar esses dados, você pode refletir se seus gastos estão alinhados com suas prioridades.
Na verdade, pesquisas mostram que pessoas que pensam a longo prazo tendem a economizar mais, enquanto aquelas focadas na gratificação imediata são mais propensas a gastar demais. Analisar seus dados de gastos pode ajudá-lo a tomar melhores decisões financeiras e construir hábitos financeiros mais saudáveis.
Usando a Tendência Central para Analisar Dados de Gastos
Ao analisar gastos, três medidas-chave de tendência central—média, mediana e moda—ajudam a resumir seu comportamento financeiro:
- Média: A média de todos os seus gastos. Embora útil, a média pode ser distorcida por valores extremos (como alguém gastando muito mais ou menos do que os outros).
- Mediana: O valor do meio quando todos os dados estão organizados em ordem. Isso dá uma ideia melhor dos gastos típicos, evitando valores atípicos.
- Moda: O valor mais frequente. Isso pode ajudar a identificar hábitos comuns ou tendências populares em gastos.
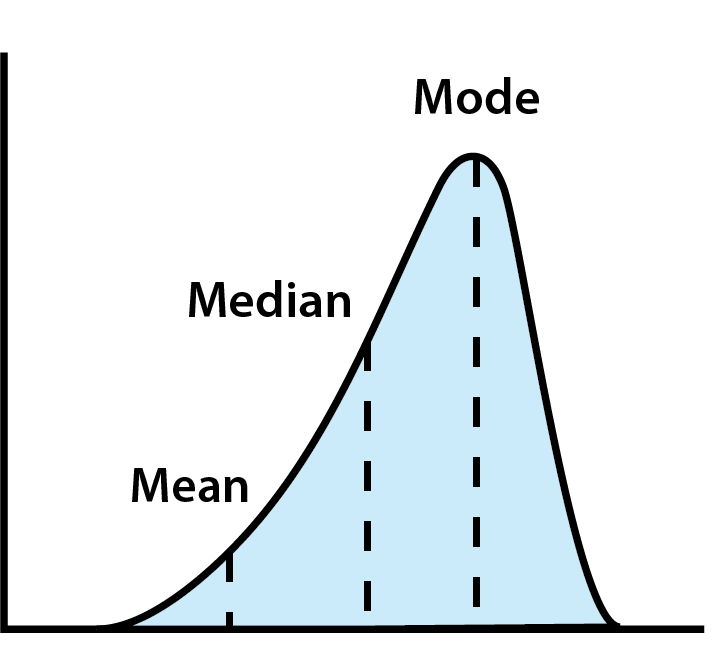
Usando a Tendência Central para Analisar Dados de Gastos
Olhar para a tendência central pode ajudar a colocar seu próprio orçamento em perspectiva. Por exemplo, você pode comprar um café todas as manhãs a caminho da escola ou do trabalho. Você percebe que isso pode somar, mas acha que está gastando mais ou menos o mesmo que a próxima pessoa (ou garota), então é uma despesa razoável.
Mas se você realmente perguntar a um grupo de seus colegas quanto eles gastam, isso pode lhe dar uma perspectiva maior de quanto você está realmente gastando a cada mês.
- Média: Se você descobrir que está gastando mais ou menos o mesmo que a média, então você estava certo sobre seus próprios hábitos de gastos. Mas se descobrir que está gastando muito mais do que todo mundo, pode ser que você olhe mais de perto suas escolhas de bebidas.
- Mediana: A mediana lhe diz como suas ações se encaixam com as de todos os outros. Talvez várias pessoas gastem $0 em café – isso faria a média ser menor do que o que o bebedor típico de café gasta. Nesse caso, você pode ver que na verdade gasta menos do que a mediana, então seus gastos são de fato razoáveis.
- Moda: O valor mais frequente. Talvez um grupo de amigos esteja pedindo o mesmo Orange Mocha Frappuccino todas as manhãs – tornando-o a escolha da moda. Se você sabe que o Orange Mocha Frappuccino é caro, isso pode significar que a mediana também está distorcida para cima do que você pensa que um bebedor típico de café está pedindo.
Exemplo: O Hábito de Café do Esteban
Esteban compra um café de $4,75 todas as manhãs. Embora ele acredite que esse é um preço razoável, ele está curioso para saber se é típico. Para ter uma melhor noção do custo médio, ele pergunta a seus amigos, familiares e colegas de trabalho quanto eles gastaram em seu café da manhã. Estas são suas respostas:

| Respondente | Quanto Eles Gastaram Esta Manhã |
|---|---|
| 1 | $0.00 |
| 2 | $6.95 |
| 3 | $1.99 |
| 4 | $0.00 |
| 5 | $4.25 |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. Calculando a Média
Primeiro, Esteban quer testar sua primeira hipótese – que ele está gastando cerca da média de todos os outros. Então, ele calcularia a média, ou média aritmética. A fórmula para calcular a média é:
Média = soma das observações / contagem das observações
A fórmula também pode ser escrita no que é chamado de Notação Sigma:
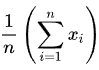
Com a Notação Sigma, o sinal Sigma (Σ) significa “somar”, o sinal n significa quantas observações, o x significa para uma observação específica, e o i significa para cada observação. Então, o que isso está dizendo é que, da primeira (i = 1, na parte inferior do sigma) até a última observação (até n, que está no topo do sigma), some todos os seus valores, depois multiplique por 1/n. A Notação Sigma é muito comum em campos de pesquisa, pois mostra operações algébricas ou matemáticas sendo aplicadas a uma série inteira de números, em vez de um por vez.
Então, somamos todas as observações:
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
E divida por 15 (contagem das observações)
$78.10 / 15 = $5.21
Esteban estava certo – ele está gastando menos do que a média. Seu $4.75 é mais barato do que o valor médio de $5.21.
2. Calculando a Mediana
Para calcular a mediana, precisamos reorganizar as ordens do menor para o maior. A mediana é o número do meio.
| Respondente | Quanto Eles Gastaram Esta Manhã |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
O valor do meio (mediana) das despesas matinais de seus amigos, familiares e colegas de trabalho é na verdade $3.00, significativamente menor do que os $4.75 de Esteban. Essa descoberta faz Esteban se sentir menos confortável sobre seu hábito diário de café. Ele percebe que está gastando 50% a mais do que seus pares, mesmo que seu custo individual esteja abaixo do preço médio.
3. Calculando a Moda
Por último, Esteban quer ver qual é a escolha mais popular. Para isso, ele precisa encontrar a moda. A moda é simplesmente a observação mais comum. No caso de sua pesquisa, 5 pessoas responderam $0.00 – tornando isso a escolha mais comum (a moda). Embora não seja a maioria das pessoas, isso definitivamente tem um grande impacto nas escolhas de média e mediana. Esteban não tem certeza do que fazer com essa informação – mas há mais matemática para ajudá-lo a encontrar uma resposta!
Interpretando os Dados: Assimetria, Valores Atípicos e Distribuições
Esteban está observando problemas en su análisis que provienen de la distribución de sus respuestas – o cómo se ven sus respuestas en un gráfico.
Sesgo
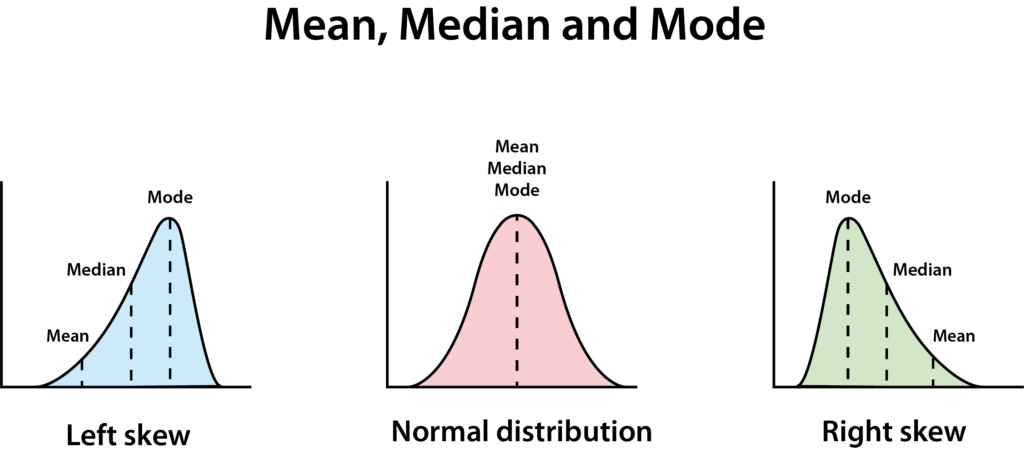
Una distribución normal tiene una forma de campana limpia. Una distribución perfectamente normal resulta en que la media, la mediana y la moda son todas iguales.
Si no son todas iguales, significa que los datos están sesgados – en este caso, decimos que sus datos tienen una distribución sesgada a la derecha, lo que significa que la mediana es menor que la media. Esto a menudo sucede cuando hay pocos números realmente grandes o realmente pequeños, haciendo que el gráfico parezca tener una larga pendiente hacia la derecha.
Valores atípicos
Cuando Esteban examina las respuestas de cerca, nota un valor atípico: un costo de $24.68. Este valor es significativamente más alto que cualquier otro. Los valores atípicos son puntos de datos que están muy alejados del resto del grupo y a menudo se excluyen del análisis estadístico porque pueden sesgar los resultados.
Tras una investigación más profunda, Esteban aprende que este valor atípico representa el costo de un galón de jugo de naranja recién exprimido comprado para toda la familia de esa persona esa mañana. Este gasto claramente no es comparable al costo típico de una sola taza de café.
Distribuciones bimodales
Las distribuciones bimodales ocurren cuando miras la distribución de frecuencias y no ves solo un pico, sino dos (o más). Echa un vistazo a estas respuestas de la encuesta sobre cuánto pagaron los estudiantes de secundaria por sus almuerzos en un día determinado:
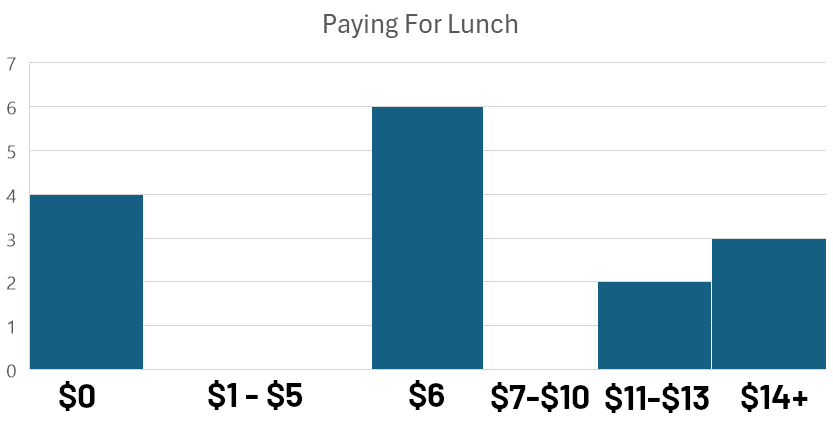
Este tipo de gráfico, donde los datos se agrupan en intervalos o ‘bins’ para comparación visual, se llama histograma. El análisis de cómo se distribuyen las observaciones dentro de estos bins se conoce como análisis de frecuencia.
Al observar el histograma, notamos dos picos distintos: uno cerca de $0 y otro cerca de $6. Esta distribución bimodal (con modos cerca de $0 y $6) sugiere que hay dos grupos distintos dentro de los datos.
Identificar estos picos puede guiar investigaciones adicionales al plantear preguntas como:
- ¿Qué factores podrían explicar estos dos patrones de gasto distintos?
- ¿Qué revelan estos picos sobre las motivaciones y comportamientos subyacentes de los individuos en estos grupos?
Además, la presencia de estos dos picos indica una distribución sesgada a la derecha, lo que significa que una mayor proporción de los puntos de datos están agrupados hacia el extremo inferior del rango de precios.
Los datos bimodales no significan necesariamente que haya dos respuestas con el mismo número exacto de observaciones, solo que podemos ver dos picos claros (en este caso, $6 es la “Moda Verdadera”).
Cuando los investigadores examinaron más de cerca los datos, la explicación se volvió obvia. $0 eran estudiantes que trajeron un almuerzo empacado de casa y $6 era el costo del almuerzo escolar regular. Los estudiantes que pagaron más de $10 estaban comprando una combinación de artículos de la cafetería de la escuela y otros alimentos que compraron en el camino a la escuela.

Conclusión: Usando datos para tomar mejores decisiones financieras
Al comprender estas tres medidas de tendencia central: media, mediana y moda, puedes interpretar datos y tomar decisiones financieras más informadas. Ya sea que estés analizando tus gastos o mirando tendencias más grandes, estas herramientas te empoderan para desarrollar mejores hábitos de dinero. Recopilar y analizar datos de gastos puede proporcionar información sobre tu comportamiento financiero.
Para estudiantes como Esteban, cambios simples—como reducir las compras discrecionales—pueden llevar a beneficios financieros a largo plazo. Cuando Esteban ve que sus gastos están por encima de la mediana – y que la opción más popular es no gastar en absoluto, ayuda a poner en contexto sus decisiones de gasto y lo que eso significa para su futuro.