Juro Composto
O Juro Composto é um dos conceitos mais importantes no mundo moderno e uma pedra angular do sistema financeiro em toda economia. O conceito de “Juro Composto” é surpreendentemente simples, mas incrivelmente poderoso!
Juro Simples
Antes de falarmos sobre o poder do Juro Composto, precisamos primeiro entender o Juro Simples.
No mundo financeiro, o Juro Simples é o retorno de um empréstimo. Por exemplo, se seu amigo pedir emprestado $100 e prometer devolver $110 em um ano, você teria um lucro de $10 ao emprestar o dinheiro. O “Juro” é a taxa de retorno, ou quanto lucro você fez como uma porcentagem do investimento original. Em termos de investimento, os $100 originais que você investiu são chamados de “Principal”.

Juro = (Devolução – Principal) / Principal
No exemplo acima, o Juro Ganho é 10%.
(110 – 100) / 100 = 10%
No mundo financeiro, o juro é geralmente expresso no retorno por ano. Se, em vez disso, seu amigo prometesse te pagar de volta em 6 meses, então a “taxa de juro anual” seria ajustada. Como 6 meses é ½ de um ano, a “taxa de juro anual” é o dobro do retorno de 6 meses.
Juro anual = Juro * Duração do empréstimo, como uma porcentagem de 1 ano
Então, se o amigo está pagando de volta em 6 meses, o Juro Anual seria 20%.
Juro anual = 10% * 2 = 20%
Portanto, dada a opção entre um retorno de 20% (seu amigo devolvendo o empréstimo, mais $10, em 6 meses) em vez de um retorno de 10% (amigo esperando 12 meses para pagar), o retorno de 20% é claramente melhor.
Juro Simples e Títulos
O investimento em títulos funciona por juro simples. Os títulos normalmente custam $1.000, e cada um deles tem uma taxa de juro e uma data de vencimento (normalmente 30 anos a partir da data de emissão).
Se você comprasse um título de $1.000, esse título pagará $50 todo ano, durante 30 anos. No final do 30º ano, você receberá o último pagamento de $50, mais seu Principal original de $1.000 de volta – um pagamento simples de juro de 5% todo ano.

Juro Simples vs Juro Composto
O juro simples é apenas isso – simples. O juro composto é um pouco mais complicado à primeira vista. Com o juro composto, em vez de simplesmente pagar o pagamento de juro no final do empréstimo, o valor da “devolução” é reinvestido.
Vamos pensar de volta ao nosso exemplo do amigo pedindo emprestado $100. Quando ele vem nos pagar de volta em 1 ano, assim que ele entrega os $110, ele pede para emprestar aqueles $110 por mais um ano, e pagar os mesmos 10% de juro. Isso significa que no final do próximo ano, seu “pagamento de juro” será $110 * 10% = $11, então o total que ele pagará de volta será $121.
Porque o amigo estava pegando emprestado o valor total – incluindo o juro do primeiro ano, a recompensa é maior! Isso significa que a cada ano, a “devolução” de cada empréstimo é adicionada ao valor original do empréstimo, “compostando” o principal (e o juro ganho) no próximo ano.
Exemplos de Juro Composto
O Juro Composto é comumente usado com poupança e investimento. Uma conta de poupança é um exemplo clássico de juro composto. Seu banco pagará juro sobre suas economias todo mês – e esse juro é depositado na própria conta de poupança. Isso significa que no próximo mês, ele ganhará juro tanto sobre o depósito original, quanto sobre o juro ganho no primeiro mês.
Investir no mercado de ações também é considerado uma forma de juro composto. Se o valor de um investimento sobe 10% a cada ano, isso significa que os retornos de um ano anterior estão incluídos nos ganhos!
A Regra dos 72
A Regra dos 72 é uma maneira simples de estimar quanto tempo levará para seu investimento dobrar com juro composto. Você apenas divide 72 pela taxa de juro anual (em forma percentual) – isso te diz exatamente quanto tempo levará para o investimento original dobrar!
| Taxa de Juros | Tempo Para Dobrar |
|---|---|
| 1% | 72 Anos |
| 2% | 36 Anos |
| 5% | 14.4 Anos |
| 10% | 7.2 Anos |
| 20% | 3.6 Anos |
Juros Compostos vs Juros Simples – Na Prática
Agora vimos como os juros simples, com um título, e os juros compostos, com uma conta de poupança, funcionam. Mas para ver por que os juros compostos são tão poderosos, vamos olhar uma comparação de 30 anos (o tempo médio de expiração de um título) para ver a diferença no retorno entre nossos dois investimentos.
Juros Simples
| Ano | Principal | Juros Ganhos |
| 1 | $ 1,000 | $50 |
| 2 | $ 1,000 | $50 |
| 3 | $ 1,000 | $50 |
| 4 | $ 1,000 | $50 |
| 5 | $ 1,000 | $50 |
| 6 | $ 1,000 | $50 |
| 7 | $ 1,000 | $50 |
| 8 | $ 1,000 | $50 |
| 9 | $ 1,000 | $50 |
| 10 | $ 1,000 | $50 |
| 11 | $ 1,000 | $50 |
| 12 | $ 1,000 | $50 |
| 13 | $ 1,000 | $50 |
| 14 | $ 1,000 | $50 |
| 15 | $ 1,000 | $50 |
| 16 | $ 1,000 | $50 |
| 17 | $ 1,000 | $50 |
| 18 | $ 1,000 | $50 |
| 19 | $ 1,000 | $50 |
| 20 | $ 1,000 | $50 |
| 21 | $ 1,000 | $50 |
| 22 | $ 1,000 | $50 |
| 23 | $ 1,000 | $50 |
| 24 | $ 1,000 | $50 |
| 25 | $ 1,000 | $50 |
| 26 | $ 1,000 | $50 |
| 27 | $ 1,000 | $50 |
| 28 | $ 1,000 | $50 |
| 29 | $ 1,000 | $50 |
| 30 | $ 1,000 | $50 |
| Total | $1,500 |
Juro Composto
| Ano | Principal | Juro Ganho |
| 1 | $ 1,000 | $ 50 |
| 2 | $ 1,050 | $ 53 |
| 3 | $ 1,103 | $ 55 |
| 4 | $ 1,158 | $ 58 |
| 5 | $ 1,216 | $ 61 |
| 6 | $ 1,276 | $ 64 |
| 7 | $ 1,340 | $ 67 |
| 8 | $ 1,407 | $ 70 |
| 9 | $ 1,477 | $ 74 |
| 10 | $ 1,551 | $ 78 |
| 11 | $ 1,629 | $ 81 |
| 12 | $ 1,710 | $ 86 |
| 13 | $ 1,796 | $ 90 |
| 14 | $ 1,886 | $ 94 |
| 15 | $ 1,980 | $ 99 |
| 16 | $ 2,079 | $ 104 |
| 17 | $ 2,183 | $ 109 |
| 18 | $ 2,292 | $ 115 |
| 19 | $ 2,407 | $ 120 |
| 20 | $ 2,527 | $ 126 |
| 21 | $ 2,653 | $ 133 |
| 22 | $ 2,786 | $ 139 |
| 23 | $ 2,925 | $ 146 |
| 24 | $ 3,072 | $ 154 |
| 25 | $ 3,225 | $ 161 |
| 26 | $ 3,386 | $ 169 |
| 27 | $ 3,556 | $ 178 |
| 28 | $ 3,733 | $ 187 |
| 29 | $ 3,920 | $ 196 |
| 30 | $ 4,116 | $ 206 |
| Total | $3,322 |
Neste exemplo, você pode ver que o Juros Compostos dá mais do que o dobro do retorno total dos juros simples – isso é poderoso! Se você olhar para um gráfico do valor total do seu investimento, você também pode ver uma diferença clara na forma:
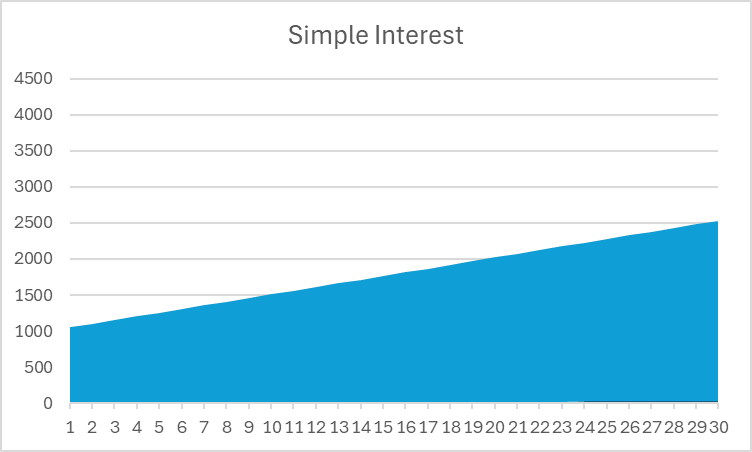
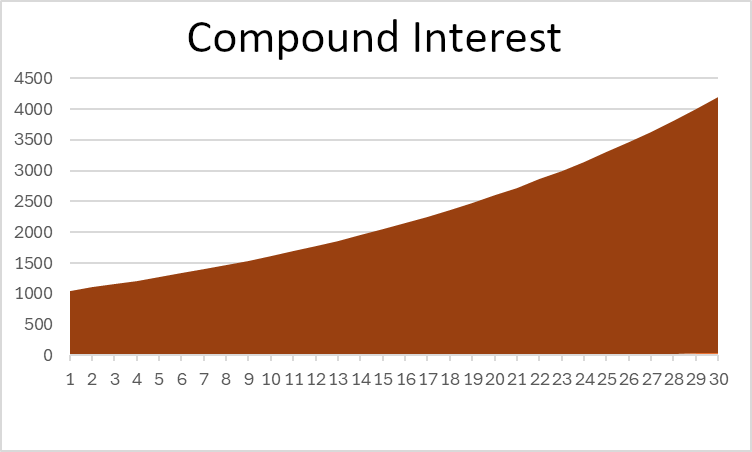
Note que os juros simples formam uma linha reta, enquanto os juros compostos curvam-se para cima ao longo do tempo.
O Caso dos Juros Simples
Embora você definitivamente queira que suas economias se acumulem ao longo do tempo para obter um melhor retorno a longo prazo, isso não significa que os juros simples devem ser ignorados. Isso apenas significa que, se você quiser que as economias se acumulem, você tem um pouco mais de trabalho a fazer.
Considere investir em Títulos, por exemplo. Enquanto os Títulos pagam juros simples, você pode pegar esses pagamentos e reinvesti-los em outro lugar (como depositar em uma conta de poupança ou comprar mais títulos) – dando a si mesmo “retornos compostos”, mesmo que tenha juros simples.
Desde que você continue a reinvestir seus retornos (não gastá-los ou mantê-los como dinheiro), você está sempre acumulando!
Frequência de Acumulação
Há uma última consideração com os Juros Compostos que pode tornar as coisas um pouco mais complicadas – a Frequência de Acumulação.
Menção anterior de que uma conta de poupança paga juros mensalmente – mesmo que use uma taxa de juros anual de 5%. Isso significa que seu banco realmente pagará 5% / 12 de juros todo mês (ou cerca de 0,42%).
Isso significa que sua conta bancária está acumulando a uma taxa de juros mais baixa, mas com uma frequência maior, do que uma conta bancária diferente que paga seus juros anualmente. Como sua conta acumula com mais frequência, isso significa que seu retorno “efetivo” é um pouco maior – com uma taxa de juros de 5% e $1.000 economizados, acumular uma vez renderia $1.050, mas acumular mensalmente termina com cerca de $1051,16. Esse extra de $1,16 não é muito – mas também não é nada.

Fórmula dos Juros Compostos
Graças ao poder dos Expoentes, podemos calcular o saldo final de um investimento em juros compostos sem calcular manualmente a cada ano, como fizemos acima. A fórmula é:
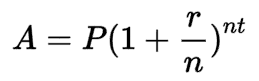
Onde:
- A é o saldo final
- P é o principal inicial
- r é a taxa de juros (em finanças, normalmente a taxa de juros anual)
- n é o número de períodos que o investimento compõe
- E t é o número de períodos de tempo que estamos medindo.
No nosso exemplo de composição anual por 30 anos, P seria $1.000, r seria 5%, n seria 1 (uma composição por ano), e t seria 30, por 30 anos. Se estivéssemos calculando juros mensais, “n” seria 12, já que compõe 12 vezes por ano.
Você pode ver a diferença entre diferentes tipos de composição com diferentes taxas de juros brincando com nosso Calculadora de Juros Compostos!
Return To Glossary