9-08 Preço de Opções – Modelo Black-Scholes
Qualquer discussão sobre opções e preços de opções estaria incompleta sem uma menção ao Black-Scholes modelo de precificação de opções.
Os acadêmicos Fischer Black e Myron Scholes, em um artigo que escreveram em 1973, afirmaram sua teoria de que uma opção era implícita na precificação de qualquer título negociado.
Referenciando o trabalho de alguns dos economistas mais famosos, como Paul Samuelson, Black e Scholes desenvolveram não uma, mas três “posições” para sua consideração.
- O Modelo Black-Scholes: Um cálculo matemático sobre ações (stocks).
- A PDE (Equação Diferencial Parcial) de Black-Scholes: Isso rastreia o movimento ou a movimentação de uma certa ação.
- A Fórmula Black-Scholes: Isso tenta calcular os preços para opções de venda e opções de compra.
A menos que você seja um matemático dedicado e sem esperança, você precisa apenas saber como o trabalho de Black-Scholes pode afetar suas atividades de investimento. Embora muitos especialistas afirmem as limitações dessa teoria, você pode adotar as previsões e projeções oferecidas pelos cálculos de Black-Scholes para ajudar sua atividade de opções.
A fórmula Black-Scholes é usada para obter o preço de opções de venda e compra europeias. Ela é obtida resolvendo a PDE de Black-Scholes – veja a derivação abaixo.
Usando esta fórmula, o valor de uma opção de compra em termos dos parâmetros de Black-Scholes é:
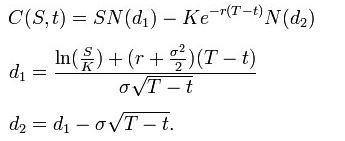
O preço de uma opção de venda é:
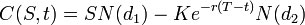
Para ambos, como acima:
- N(•) é a função de distribuição acumulada da distribuição normal padrão
- T – t é o tempo até o vencimento
- S é o preço à vista do ativo subjacente
- K é o preço de exercício
- r é a taxa livre de risco (taxa anual, expressa em termos de capitalização contínua)
- σ é a volatilidade nos log-retornos do subjacente

