Limites et journaux – Dépenses et économies personnalisées
Une grande partie des finances personnelles est axée sur la pensée à long terme : établir votre budget afin de pouvoir économiser suffisamment d’argent pour vivre le style de vie que vous souhaitez et prendre votre retraite confortablement.
Mais pour chaque personne, « un style de vie que vous souhaitez » et « prendre sa retraite confortablement » peuvent signifier des choses très différentes. À la fin de la journée, chaque personne prend une décision chaque mois sur combien elle va dépenser (ou consommer) et combien elle va économiser (ou investir).
En comprenant le processus de réflexion derrière ce compromis, vous pouvez obtenir une image plus claire de vos propres dépenses. Cela vous aidera à vous assurer que vos dépenses réelles correspondent à vos dépenses prévues.
Modélisation de la consommation – Rendements décroissants à l’échelle
Une grande partie des mathématiques financières se concentre sur la croissance exponentielle – comment un investissement croît en fonction d’un taux d’intérêt, comment un compte d’épargne croît au fil du temps, ou comment construire une richesse à long terme. Les fonctions exponentielles ont une courbe ascendante – les investissements deviennent plus importants avec le temps :

Mais lorsque vous dépensez au lieu d’épargner, le bénéfice que vous obtenez pour chaque dollar que vous dépensez n’a pas cette courbe ascendante. Au lieu de cela, les économistes disent que la consommation a des rendements décroissants à l’échelle.
Pensez-y de cette façon – vous voyez deux appartements à louer. L’un a une chambre, les appareils ont 30 ans, la salle de bain est minuscule, et la cuisine n’a même pas de place pour une table. Cet appartement est proposé à 500 $ / mois.
Le deuxième appartement a des appareils flambant neufs, une salle de bain spacieuse avec une baignoire et une douche séparées, et la cuisine a des comptoirs en granit avec à la fois de l’espace pour une table et un bar à petit-déjeuner. Celui-ci est proposé à 1 500 $ / mois.
Maintenant, le deuxième appartement peut très bien valoir 1 000 $ de plus par mois. Mais la valeur que vous recevez en ayant un appartement (un endroit pour dormir la nuit, stocker vos affaires en toute sécurité, cuisiner et manger, etc.) est la partie la plus importante. Si vous essayiez de décomposer tous les différents équipements que vous obtenez avec l’appartement plus cher pour voir d’où vient toute la valeur, cela pourrait ressembler à ceci :
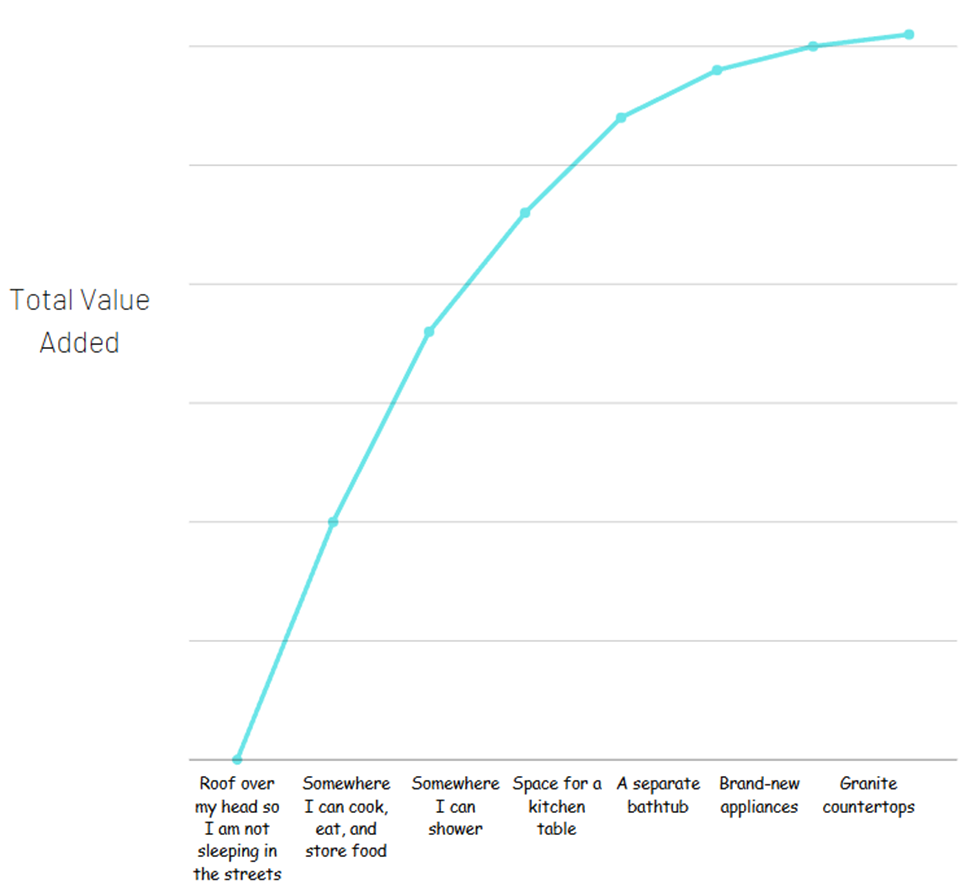
La plupart de la valeur totale provient des bases des bases. Cela ne signifie en aucun cas que les extras ne valent pas le coup – il n’y a pas de signes dollar ici, juste combien de valeur vous obtenez.
En économie, ce concept est appelé utilité – la satisfaction ou le bénéfice dérivé de la consommation de biens ou de services. Vous remarquerez que la courbe s’aplatit à mesure que les dépenses augmentent. Pour modéliser cela mathématiquement, nous utilisons des logarithmes au lieu d’exposants.
Qu’est-ce qu’un logarithme ?
Vous pouvez penser aux logarithmes en relation avec les exposants de la même manière que la division est liée à la multiplication – c’est la fonction mathématique opposée. En d’autres termes,
Si 2^3 = 8, alors 3 est le logarithme de 8 à la base 2.
En économie et en finance, les logarithmes sont utiles pour montrer ces rendements décroissants à l’échelle pour les dépenses. Par exemple, si nous voulons faire un graphique montrant l’utilité reçue pour la consommation pendant un mois donné, le graphique pourrait ressembler à ceci :
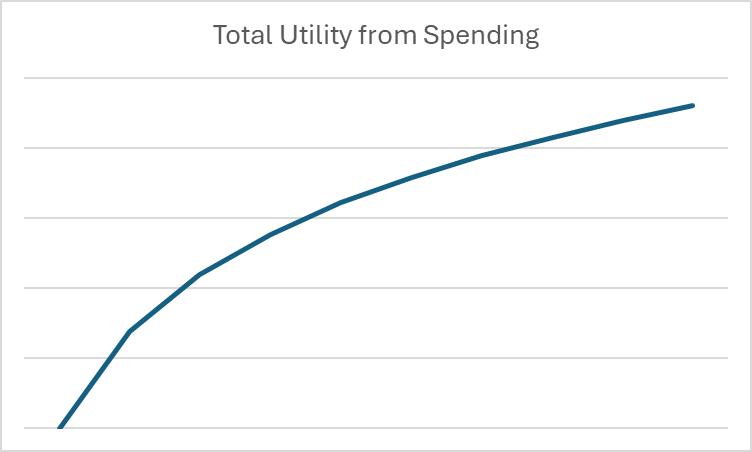
Une fois que nous plaçons nos dépenses dans le contexte des logarithmes et de l’utilité, nous pouvons commencer à examiner les décisions de dépenses et d’épargne à long terme purement en mathématiques.
Valeur temporelle de l’argent – Taux d’actualisation
La valeur temporelle de l’argent fait référence au fait qu’un dollar dans le futur vaut moins qu’un dollar aujourd’hui. Cela est dû au fait qu’entre maintenant et le futur, j’aurais pu utiliser ce dollar pour faire quelque chose – et cette opportunité pourrait être passée.
Lorsque nous voulons décrire mathématiquement la valeur temporelle de l’argent, nous utilisons quelque chose appelé un taux d’actualisation. Le taux d’actualisation est un simple nombre entre 0 et 1 qui répond à cette question :
Combien seriez-vous prêt à renoncer aujourd’hui pour obtenir 1 $ dans 1 mois ?

Le taux d’actualisation de chaque personne est différent – il fait référence à la manière dont leurs préférences personnelles sont à court ou à long terme. Comme vous pouvez vous y attendre, une personne avec un taux d’actualisation élevé (disons, 0,9) est beaucoup plus susceptible d’être un épargnant qu’une personne avec un taux d’actualisation bas (disons, 0,3). C’est parce qu’une personne avec un taux d’actualisation bas valorise beaucoup d’avoir cet argent tout de suite – donc elle est prête à renoncer à 70 % de sa valeur pour l’obtenir immédiatement au lieu d’attendre.
Le taux d’actualisation est généralement exprimé avec la lettre grecque β. Donc, si votre taux d’actualisation personnel est de 0,95, nous dirions β = 0,95.
Taux d’actualisation et exposants
Une fois que vous pouvez identifier votre propre taux d’actualisation personnel, vous pouvez également l’utiliser pour déterminer combien vous prendriez pour ce dollar s’il est encore plus loin dans le futur en utilisant des exposants.
En élevant votre bêta par un exposant égal à la distance dans le futur que nous voulons calculer, nous pouvons dire combien ce dollar vaut aujourd’hui. En d’autres termes, β ^t = combien vous seriez prêt à prendre aujourd’hui en échange d’un dollar t mois à partir de maintenant.
Dans notre exemple de β = 0.95, voici ce qu’un dollar vaut au cours de l’année suivante :
| Moins dans le futur | Combien vous seriez prêt à prendre aujourd’hui pour sacrifier 1 $ dans le futur |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
Cela signifie que si votre β = 0.95, vous seriez prêt à prendre 0,54 $ pour sacrifier un dollar dans un an.
Maintenant que nous avons le concept de logarithmes et de taux d’actualisation, nous pouvons le rassembler pour voir ce que cela signifie pour les décisions d’épargne et de dépense à long terme !
Utilité à Vie
La plupart de ce que vous apprenez dans un cours de finance personnelle concerne l’épargne pour l’avenir, en particulier la retraite. Mais ce n’est pas vraiment votre objectif financier dans la vie – vous voulez vraiment maximiser votre utilité totale à vie. C’est pourquoi personne ne sauve chaque centime – vous équilibrez votre bénéfice (ou utilité) de dépenser aujourd’hui contre la croissance de votre richesse (grâce à la puissance des intérêts composés) afin de pouvoir la dépenser à l’avenir.
Cela signifie qu’à chaque mois de votre vie, vous avez votre revenu pour ce mois, plus toutes les économies que vous avez accumulées jusqu’à présent. Ces ressources combinées sont ce que vous avez à votre disposition. Vous décidez consciemment combien de ces ressources vous allez dépenser (ou consommer) et combien vous allez épargner (ou investir). Vous avez également une certaine compréhension du taux d’intérêt auquel vos économies vont croître au fil du temps. En termes mathématiques, vous choisissez c et i où :
I + (s x (1 + r)) = c + i
Où ces variables se réfèrent à :
- I = votre revenu ce mois-ci
- s = combien vous avez déjà épargné/investi au début du mois
- r = le taux d’intérêt auquel vos économies croissent. Ainsi, vos économies du mois dernier auront un peu augmenté d’ici le début de ce mois par rapport à ce que vous aviez le mois dernier.
- c = combien vous consommez/dépensez ce mois-ci
- i = combien vous épargnez/investissez ce mois-ci
Le bénéfice que vous tirez de la consommation peut être exprimé en prenant le logarithme de votre consommation :
Utilité = log(c)
Vous devez déterminer combien dépenser (et par conséquent épargner) à chaque période pour maximiser votre utilité totale à vie, pas seulement votre bonheur dans l’instant présent. En utilisant votre taux d’actualisation et des exposants, nous pouvons calculer l’utilité que vous obtiendrez de la consommation à n’importe quelle période dans le futur, puis les additionner toutes.
Utilité Totale à Vie =
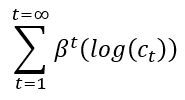
Limites – L’approche de l’utilité et des remises tend vers zéro
Au départ, cela semble infini – nous additionnons des nombres infinis, donc cela pourrait devenir de plus en plus grand pour toujours. Cependant, parce que t continue de croître, cela signifie que la remise appliquée dans un avenir lointain commence à se rapprocher TRÈS près de zéro.
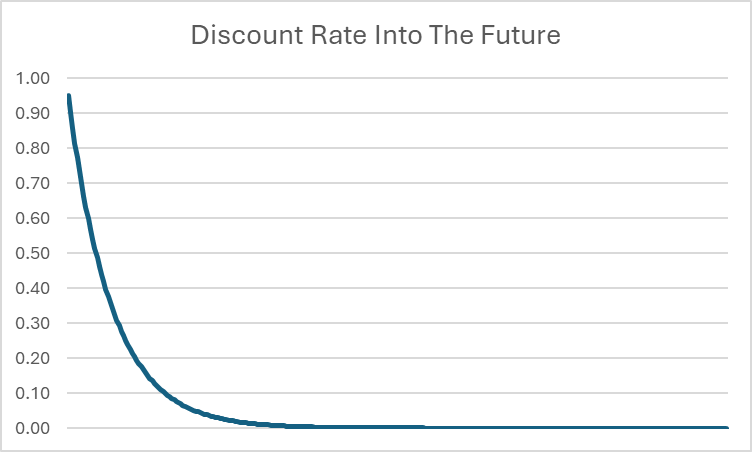
Par exemple, même si β = 0,95, le taux de remise dans 20 ans est réduit à 0,0000045. Plus on s’éloigne dans le futur, plus le taux de remise se rapproche de 0. Bien que le montant exact maximum de la consommation à vie puisse être impossible à calculer avec une précision absolue (car cela pourrait théoriquement impliquer un nombre infini de décimales), nous pouvons affirmer avec confiance qu’il existe une limite supérieure au montant total de consommation atteignable au cours d’une vie.
Les limites sont utilisées pour définir ces bornes supérieures et inférieures. Nous pouvons dire en toute sécurité que le taux de remise a une limite inférieure de 0 à mesure que t continue de croître vers l’infini – il continuera à se rapprocher de 0, mais ne l’atteindra jamais. La limite supérieure de l’utilité totale à vie peut également être calculée (mais cela nécessite des calculs avancés, qui ne font pas partie de cette leçon).
Taux de remise et taux d’intérêt – Choisir d’épargner
Une fois que nous dépassons tous les calculs, ce que nous pouvons vraiment voir, c’est que la décision de dépenser ou d’épargner repose vraiment sur seulement deux variables :
- Votre propre taux de remise personnel (ou β)
- Le taux d’intérêt r, qui détermine combien vos investissements vont croître
S’il y a deux personnes qui s’attendent au même retour sur investissement pour leurs économies, mais que nous observons qu’une personne est un grand épargnant et l’autre un grand dépensier, nous pouvons dire que l’épargnant a un β plus élevé que le dépensier – nous pouvons utiliser un chiffre réel pour quantifier À QUEL POINT quelqu’un est épargnant ou dépensier.

Une bonne compréhension des taux d’intérêt est cruciale pour la littératie financière. Si votre seule option d’épargne est un compte d’épargne à faible intérêt (peut-être ne rapportant que 3 % par an), vous êtes moins susceptible de donner la priorité aux objectifs d’épargne à long terme. Cela est dû au fait que vous pourriez ne pas saisir pleinement le potentiel des investissements à risque plus élevé et à rendement plus élevé comme le marché boursier.
En fin de compte, l’aspect le plus important de la littératie financière est d’être conscient des options d’investissement qui s’offrent à vous et de prendre des décisions éclairées en fonction de vos circonstances individuelles et de votre tolérance au risque.