Dépenses discrétionnaires – Comprendre la tendance centrale
Qu’est-ce que les dépenses discrétionnaires ?
Les dépenses discrétionnaires sont des achats non essentiels— demandes, des choses que nous achetons pour le plaisir, la commodité ou le divertissement. Des exemples incluent le divertissement, les repas au restaurant ou les derniers gadgets technologiques. En revanche, les besoins sont essentiels à la survie : nourriture, logement, services publics et soins de santé. Connaître la différence entre les besoins et les demandes est une compétence financière clé, surtout lorsque vous commencez à gérer votre propre argent.

Pourquoi c’est important
Comprendre la différence entre les besoins et les demandes vous aide à faire des choix financiers plus intelligents. Par exemple, si vous avez économisé pour un nouveau jeu vidéo mais que votre téléphone se casse, que choisissez-vous ? Le téléphone est un besoin ; le jeu est une demande. Choisir de remplacer le téléphone garantit que vous couvrez une dépense nécessaire, vous préparant à la sécurité financière à long terme.
Analyser les besoins vs. les demandes : une approche basée sur les données
Suivre vos dépenses aide à révéler des modèles dans vos habitudes financières. Vous pourriez suivre combien vous et vos amis dépensez pour des articles non essentiels comme des collations, des divertissements ou des applications. En examinant ces données, vous pouvez réfléchir à la manière dont vos dépenses s’alignent sur vos priorités.
En fait, des recherches montrent que les personnes qui pensent à long terme ont tendance à économiser davantage, tandis que celles qui se concentrent sur la gratification immédiate sont plus susceptibles de dépenser trop. Analyser vos données de dépenses peut vous aider à prendre de meilleures décisions financières et à construire des habitudes financières plus saines.
Utiliser la tendance centrale pour analyser les données de dépenses
Lors de l’analyse des dépenses, trois mesures clés de tendance centrale—moyenne, médiane et mode—aident à résumer votre comportement financier :
- Moyenne : La moyenne de toutes vos dépenses. Bien que utile, la moyenne peut être biaisée par des valeurs extrêmes (comme quelqu’un dépensant beaucoup plus ou moins que les autres).
- Médiane : La valeur médiane lorsque toutes les données sont classées par ordre. Cela donne une meilleure idée des dépenses typiques en évitant les valeurs aberrantes.
- Mode : La valeur la plus fréquente. Cela peut aider à identifier des habitudes courantes ou des tendances populaires dans les dépenses.
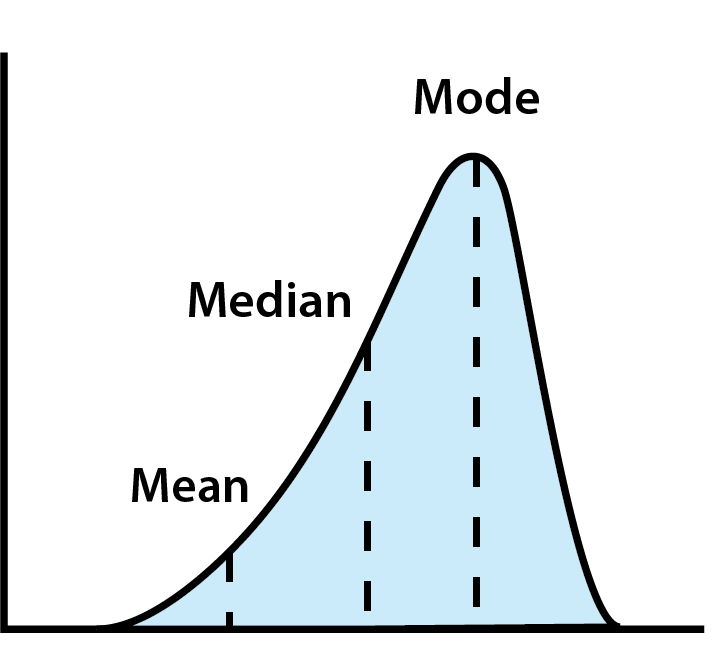
Utiliser la tendance centrale pour analyser les données de dépenses
Regarder la tendance centrale peut aider à mettre votre propre budget en perspective. Par exemple, vous pourriez acheter un café chaque matin en allant à l’école ou au travail. Vous réalisez que cela peut s’accumuler, mais vous pensez que vous dépensez à peu près autant que la personne suivante (ou la suivante), donc c’est une dépense raisonnable.
Mais si vous demandez réellement à un groupe de vos pairs combien ils dépensent, cela peut vous donner une plus grande perspective sur combien vous dépensez réellement chaque mois.
- Moyenne : Si vous découvrez que vous dépensez à peu près autant que la moyenne, alors vous aviez raison sur vos propres habitudes de dépenses. Mais si vous constatez que vous dépensez beaucoup plus que tout le monde, vous pourriez examiner de plus près vos choix de boissons.
- Médiane : La médiane vous indique comment vos actions s’inscrivent par rapport à tout le monde. Peut-être que plusieurs personnes dépensent 0 $ pour le café – cela ferait baisser la moyenne par rapport à ce que dépense un buveur de café typique. Dans ce cas, vous pourriez voir que vous dépensez en fait moins que la médiane, donc vos dépenses sont en effet raisonnables.
- Mode : La valeur la plus fréquente. Peut-être qu’un groupe d’amis commande le même Orange Mocha Frappuccino ensemble chaque matin – en faisant de cela le choix mode. Si vous savez que l’Orange Mocha Frappuccino est cher, cela pourrait signifier que la médiane est également biaisée plus haut que ce que vous pensez qu’un buveur de café typique commande.
Exemple : L’habitude de café d’Esteban
Esteban achète un café à 4,75 $ chaque matin. Bien qu’il pense que c’est un prix raisonnable, il est curieux de savoir si c’est typique. Pour avoir une meilleure idée du coût moyen, il demande à ses amis, sa famille et ses collègues combien ils ont dépensé pour leur café du matin. Voici leurs réponses :

| Répondant | Combien ils ont dépensé ce matin |
|---|---|
| 1 | 0,00 $ |
| 2 | 6,95 $ |
| 3 | 1,99 $ |
| 4 | 0,00 $ |
| 5 | 4,25 $ |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. Calculer la moyenne
Tout d’abord, Esteban veut tester sa première hypothèse – qu’il dépense environ la moyenne de tout le monde. Donc, il calculerait la moyenne, ou la moyenne arithmétique. La formule pour calculer la moyenne est :
Moyenne = somme des observations / nombre d’observations
La formule peut également être écrite dans ce qu’on appelle la notation sigma :
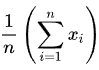
Avec la notation sigma, le signe sigma (Σ) signifie “additionner”, le signe n signifie combien d’observations, le x signifie pour une observation spécifique, et le i signifie pour chaque observation. Donc, ce que cela signifie, c’est que de la première (i = 1, en bas du sigma) à la dernière observation (jusqu’à n, qui est en haut du sigma), additionnez toutes leurs valeurs, puis multipliez par 1/n. La notation sigma est très courante dans les domaines de recherche, car elle montre des opérations algébriques ou mathématiques appliquées à une série entière de nombres, au lieu d’un à la fois.
Alors, nous additionnons toutes les observations :
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
Et divisez par 15 (nombre d’observations)
$78.10 / 15 = $5.21
Esteban avait raison – il dépense moins que la moyenne. Ses $4.75 sont moins chers que la valeur moyenne de $5.21.
2. Calculer la médiane
Pour calculer la médiane, nous devons réorganiser les ordres du plus petit au plus grand. La médiane est le nombre du milieu.
| Répondant | Combien ils ont dépensé ce matin |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
La valeur médiane des dépenses en café du matin de ses amis, de sa famille et de ses collègues est en fait de $3.00, significativement inférieure aux $4.75 d’Esteban. Cette découverte rend Esteban moins à l’aise avec son habitude quotidienne de café. Il réalise qu’il dépense 50 % de plus que ses pairs, même si son coût individuel est inférieur au prix moyen.
3. Calculer le mode
Enfin, Esteban veut voir quel est le choix le plus populaire. Pour cela, il doit trouver le mode. Le mode est simplement l’observation la plus courante. Dans le cas de son enquête, 5 personnes ont répondu $0.00 – ce qui en fait le choix le plus courant (le mode). Bien que ce ne soit pas la majorité des personnes, cela a certainement un grand impact sur les choix de la moyenne et de la médiane. Esteban n’est pas tout à fait sûr de ce qu’il doit faire avec cette information – mais il y a plus de mathématiques pour l’aider à trouver une réponse !
Interpréter les données : Asymétrie, valeurs aberrantes et distributions
Esteban examine les problèmes dans son analyse provenant de la distribution de ses réponses – ou comment ses réponses apparaissent sur un graphique.
Asymétrie
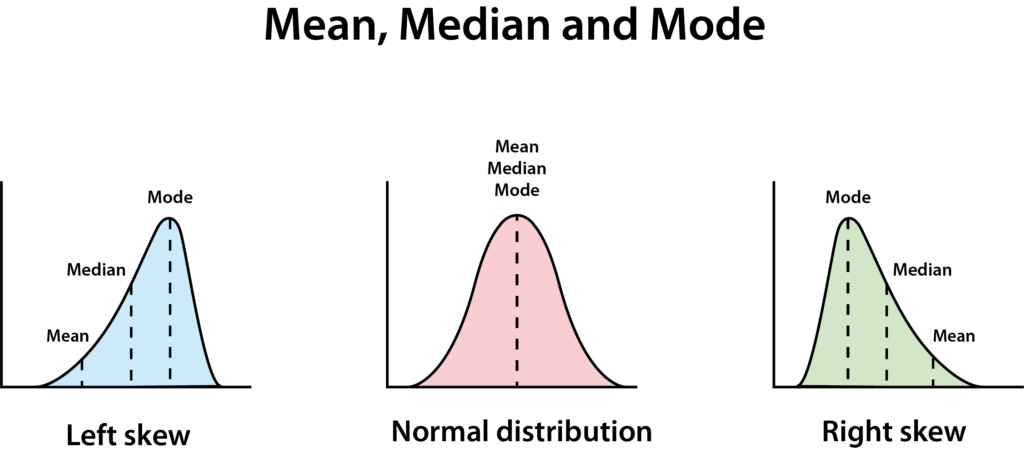
Une distribution normale a une forme de cloche nette. Une distribution parfaitement normale entraîne la moyenne, la médiane et le mode étant tous égaux.
S’ils ne sont pas tous égaux, cela signifie que les données sont asymétriques – dans ce cas, nous disons que ses données ont une distribution asymétrique à droite, ce qui signifie que la médiane est inférieure à la moyenne. Cela se produit souvent lorsqu’il y a peu de très grands ou très petits nombres, ce qui donne au graphique l’apparence d’une longue pente allant vers la droite.
Valeurs aberrantes
Lorsque Esteban examine les réponses de près, il remarque une valeur aberrante : un coût de 24,68 $. Cette valeur est significativement plus élevée que toute autre. Les valeurs aberrantes sont des points de données qui sont très éloignés du reste du groupe et sont souvent exclues de l’analyse statistique car elles peuvent fausser les résultats.
Après une enquête plus approfondie, Esteban apprend que cette valeur aberrante représente le coût d’un gallon de jus d’orange fraîchement pressé acheté pour toute la famille de cette personne ce matin-là. Cette dépense n’est clairement pas comparable au coût typique d’une seule tasse de café.
Distributions bimodales
Les distributions bimodales se produisent lorsque vous regardez la distribution de fréquence et ne voyez pas qu’un seul pic, mais deux (ou plus). Jetez un œil à ces réponses d’enquête sur combien les élèves de lycée ont payé pour leur déjeuner un jour donné :
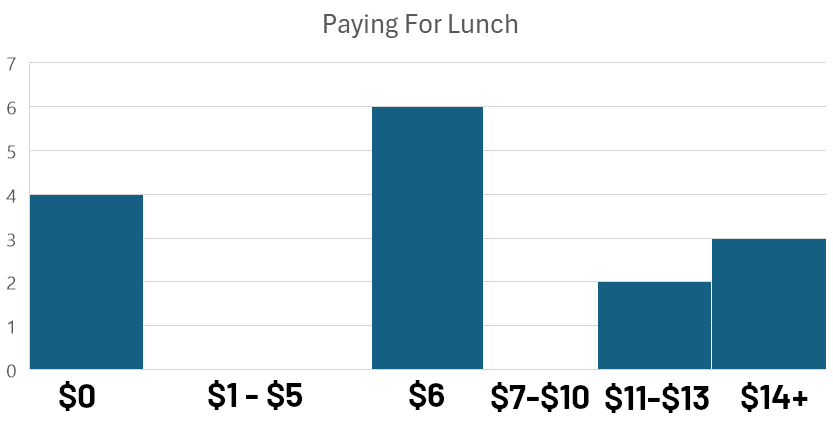
Ce type de graphique, où les données sont regroupées en intervalles ou ‘bins’ pour une comparaison visuelle, s’appelle un histogramme. L’analyse de la façon dont les observations sont distribuées dans ces bins est connue sous le nom d’analyse de fréquence.
En observant l’histogramme, nous remarquons deux pics distincts : un près de 0 $ et un autre près de 6 $. Cette distribution bimodale (avec des modes près de 0 $ et 6 $) suggère qu’il y a deux groupes distincts au sein des données.
Identifier ces pics peut guider des recherches supplémentaires en posant des questions telles que :
- Quels facteurs pourraient expliquer ces deux modèles de dépenses distincts ?
- Que révèlent ces pics sur les motivations et comportements sous-jacents des individus dans ces groupes ?
De plus, la présence de ces deux pics indique une distribution asymétrique à droite, ce qui signifie qu’une plus grande proportion des points de données sont regroupés vers le bas de l’échelle des prix.
Des données bimodales ne signifient pas nécessairement qu’il y a deux réponses avec le même nombre d’observations, juste que nous pouvons voir deux pics clairs (dans ce cas, 6 $ est le “Véritable Mode”).
Lorsque les chercheurs ont examiné de plus près les données, l’explication est devenue évidente. 0 $ était pour les étudiants qui apportaient un déjeuner préparé de chez eux et 6 $ était le coût du déjeuner scolaire régulier. Les étudiants qui ont payé plus de 10 $ achetaient une combinaison d’articles au bar à collations de l’école et d’autres aliments qu’ils avaient achetés en route pour l’école.

Conclusion : Utiliser les données pour prendre de meilleures décisions financières
En comprenant ces trois mesures de tendance centrale : moyenne, médiane et mode, vous pouvez interpréter les données et prendre des décisions financières plus éclairées. Que vous analysiez vos dépenses ou que vous regardiez des tendances plus larges, ces outils vous permettent de développer de meilleures habitudes financières. Collecter et analyser des données de dépenses peut fournir un aperçu de votre comportement financier.
Pour des étudiants comme Esteban, des changements simples – comme réduire les achats discrétionnaires – peuvent entraîner des avantages financiers à long terme. Lorsque Esteban voit que ses dépenses sont supérieures à la médiane – et que le choix le plus populaire est de ne pas dépenser du tout, cela aide à mettre en contexte ses décisions de dépenses et ce que cela signifie pour son avenir.