4-02 Mesurer le Risque : Le Ratio de Sharpe
Le Ratio de Sharpe, nommé d’après le lauréat du prix Nobel William F. Sharpe, mesure le taux de rendement en association avec le niveau de risque utilisé pour obtenir ce taux. C’est un outil particulièrement utile pour les investisseurs novices afin de suivre la “chance” par rapport à l'”intelligence”.
Un Exemple du Ratio de Sharpe
Regardez la performance de ces deux actions :
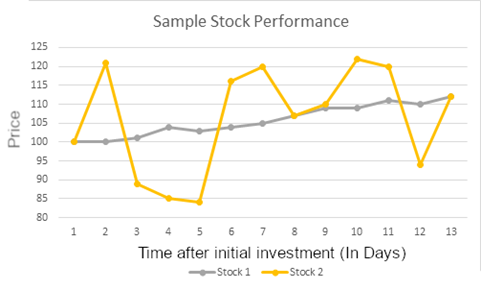
Le premier jour que nous suivons et le dernier jour, ces deux investissements ont la même valeur. Cependant, l’Action 1 est très cohérente dans ses rendements, tandis que l’Action 2 a une très large gamme de variance. Dans cet exemple, si un investisseur détient ces deux actions pendant 13 jours, leur rendement serait le même pour les deux.
Cependant, imaginez si l’investisseur vendait les deux actions le Jour 11. Le rendement de l’Action 2 serait beaucoup plus élevé ! Mais s’ils attendaient juste un jour de plus, au jour 12, la valeur de l’Action 2 s’effondrerait, donc l’Action 1 semble être un meilleur choix.
Comment Utiliser le Ratio de Sharpe Lors de l’Investissement
Lorsque vous épargnez et investissez, l’objectif doit toujours être des rendements cohérents et la préservation du capital ; vous ne voulez pas faire des mouvements risqués qui pourraient anéantir toutes les économies que vous avez mises. Un investisseur avisé préférerait l’Action A, car il n’a pas besoin de s’inquiéter de “chronométrer le marché”, au lieu de cela, il peut se concentrer sur la construction d’un portefeuille solide à long terme, au lieu de se concentrer sur le moment d’acheter et de vendre des “actions chaudes” aux meilleurs prix.
Dans cet exemple, l’Action A aurait un Ratio de Sharpe beaucoup plus élevé que l’Action B, car elle a beaucoup moins de variance pour le même rendement à la fin de la période que nous avons examinée.
Vous pouvez étendre ce concept à un portefeuille entier ; si la valeur de votre portefeuille fluctue beaucoup, mais que vous terminez avec une valeur plus élevée, vous aurez un Ratio de Sharpe beaucoup plus bas que quelqu’un d’autre qui pourrait avoir un rendement final plus bas, mais dont la valeur du portefeuille a augmenté à un rythme plus cohérent tout au long de la période de négociation.
LES DEUX mesures sont très importantes pour déterminer quel portefeuille a fait le “mieux”. Une clé de l’investissement est d’équilibrer risque et récompense ; un Ratio de Sharpe entre 1 et 2 est “bon”, entre 2 et 3 est “super”, et supérieur à 3 est “excellent”. Cependant, si vous comparez deux portefeuilles avec un Ratio de Sharpe similaire, le rendement standard vous en dira plus sur lequel était un investissement plus judicieux.

Calcul du Ratio de Sharpe
Le Ratio de Sharpe nécessite trois chiffres :
- Le rendement global en pourcentage de l’action ou du portefeuille que vous analysez
- Un taux “sans risque” (généralement ce que vous obtiendriez si vous investissiez dans des obligations d’État)
- La déviation standard des rendements quotidiens de cette action ou de ce portefeuille
Le calcul réel ressemble à ceci :

En haut, nous soustrayons le taux “sans risque” des rendements réels. Parce que nous ne nous soucions que de la façon dont l’investissement est risqué, nous voulons seulement savoir combien il a fait mieux que “sans risque”.
En bas, nous divisons tout cela par la déviation standard des rendements, qui mesure combien mon rendement quotidien a fluctué. Parce que ce chiffre est en bas du ratio, une forte variation = un faible Ratio de Sharpe. Vous pouvez calculer la Déviation Standard avec Excel, Google Sheets, ou la plupart des autres logiciels de tableur en utilisant la fonction “STDEV”.
Limitations du Ratio de Sharpe
La limitation du Ratio de Sharpe est qu’il vous dit simplement qu’un investissement était meilleur qu’un autre en comparant le risque, mais ne vous dit pas COMBIEN meilleur cet investissement était. En d’autres termes, il n’y a pas d’unités pour mesurer le bénéfice supplémentaire de choisir un investissement plutôt qu’un autre.
Par exemple, imaginez que vous ayez acheté 1000 $ d’actions ABC, et que son prix ait grimpé de 1 % en un jour – donc maintenant vous avez 1010 $. Vous vendez immédiatement l’action et achetez une obligation d’État sans risque de 1000 $, avec un rendement de 1 %.
Après un an, vous aurez gagné 10 $ de l’action ce premier jour, et encore 10 $ de votre obligation – un rendement total de 20 $, soit 2 %. Il n’y a pas beaucoup d’investisseurs qui seraient impressionnés par cela. Mais parce que vous investissiez dans des obligations sans risque pendant presque toute l’année, la variance (et la déviation standard) de votre portefeuille serait presque nulle – vous donnant un Ratio de Sharpe extrêmement élevé, peut-être supérieur à 10 !
Un autre investisseur a choisi des fonds indiciels très stables, avec un rendement annuel de 10 %. Mais parce que le prix a légèrement fluctué chaque jour, il y avait une certaine variance, et donc leur Ratio de Sharpe pourrait n’être qu’environ 3 – généralement considéré comme excellent. En comparant uniquement le Ratio de Sharpe, votre Ratio de Sharpe de 10 semble excellent, mais en réalité, l’autre investisseur a probablement pris une décision d’investissement plus judicieuse.