4-02 Riski mõõtmine: Sharpe’i suhe

Sharpe’i suhe, mis on nimetatud Nobeli preemia laureaadi William F. Sharpe’i järgi, mõõdab tootluse määra seoses riskitasemega, mida kasutatakse selle määra saavutamiseks. See on eriti kasulik tööriist algajatele investoritele, et jälgida “õnne” ja “nutikuse” suhet.

Sharpe’i suhte näide

Vaadake nende kahe aktsia tootlust:

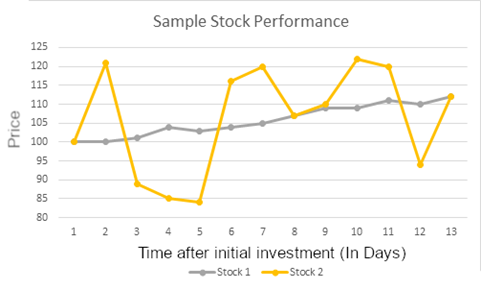
Esimesel ja viimasel päeval, mil me jälgime, on nende kahe investeeringu väärtus sama. Siiski on Aktsia 1 oma tootluses väga järjepidev, samas kui Aktsia 2-l on väga suur variatsioon. Selles näites, kui investor hoiab mõlemat aktsiat 13 päeva, oleks nende tootlus mõlemal sama.

Kuid kujutage ette, kui investor müüs mõlemad aktsiad 11. päeval. Aktsia 2 tootlus oleks palju kõrgem! Kuid kui nad ootaksid veel ühe päeva, siis 12. päeval kukuks Aktsia 2 väärtus, nii et Aktsia 1 näib olevat parem valik.

Kuidas kasutada Sharpe’i suhet investeerimisel

Kui säästate ja investeerite, peaks eesmärk alati olema järjepidev tootlus ja kapitali säilitamine; te ei soovi teha riskantseid samme, mis võivad hävitada kõik teie säästud. Tark investor eelistaks Aktsiat A, kuna nad ei pea muretsema “turule sisenemise ajastamise” pärast, vaid saavad keskenduda tugeva pikaajalise portfelli loomisele, selle asemel et keskenduda, millal osta ja müüa mõningaid “kuumi aktsiaid” parimate hindadega.

Selles näites oleks Aktsia A Sharpe’i suhe palju kõrgem kui Aktsia B, kuna selle variatsioon on sama tootluse puhul, mida me vaatasime, palju väiksem.

Saate seda kontseptsiooni laiendada kogu portfellile; kui teie portfelli väärtus kõigub palju üles ja alla, kuid te lõpetate kõrgema väärtusega, on teie Sharpe’i suhe palju madalam kui kellelgi, kellel võib olla madalam lõpptootlus, kuid kelle portfelli väärtus kasvas kauplemisperioodi jooksul järjepidevamalt.

KUIDAGI on mõlemad mõõdud väga olulised, et määrata, milline portfell tegi “parima”. Investeerimise võti on tasakaalu leidmine riski ja tasu vahel; Sharpe’i suhe vahemikus 1 kuni 2 on “hea”, vahemikus 2 kuni 3 on “suurepärane” ja üle 3 on “suurepärane”. Siiski, kui võrrelda kahte portfelli, millel on sarnane Sharpe’i suhe, ütleb standardne tootlus teile rohkem, milline oli targem investeering.

Sharpe’i suhte arvutamine

Sharpe’i suhe nõuab kolme numbrit:

1. Aktsia või portfelli üldine protsentuaalne tootlus, mida te analüüsite
2. “Riskivaba” määr (tavaliselt see, mida te saaksite, kui investeeriksite riigiväärtpaberitesse)
3. Antud aktsia või portfelli igapäevaste tootluste standardhälve

Tegelik arvutus näeb välja selline:

Ülalpool lahutame “riskivaba” määra tegelikest tootlustest. Kuna meid huvitab ainult, kui riskantne investeering on, tahame teada, kui palju paremini see toimis kui “riskivaba”.

Allpool jagame kõik selle tootluste standardhälbega, mis mõõdab, kui palju minu igapäevane tootlus üles ja alla liikus. Kuna see number on suhte allosas, kõrge variatsioon = madal Sharpe’i suhe. Saate standardhälvet arvutada Excelis, Google Sheetsis või enamikus teistes tabelarvutusprogrammidest, kasutades “STDEV” funktsiooni.

Sharpe’i suhte piirangud

Sharpe’i suhte piirang on see, et see ütleb teile lihtsalt, et üks investeering oli parem kui teine, võrreldes riski, kuid ei ütle, KUI PALJU parem see investeering oli. Teisisõnu, ei ole ühikuid, millega mõõta lisahüve, mis tuleneb ühe investeeringu valimisest teise üle.

Näiteks kujutage ette, et ostsite 1000 dollarit aktsiat ABC ja selle hind tõusis ühe päeva jooksul 1% – nüüd on teil 1010 dollarit. Te müüte kohe aktsia ja ostate 1000 dollari eest riskivaba riigiväärtpaberi, mille tootlus on 1%.

Aasta pärast olete teeninud 10 dollarit aktsiast sellel esimesel päeval ja veel 10 dollarit oma võlakirjast – kokku 20 dollarit, 2% kogutootlus. Paljusid investoreid see ei muljeta. Kuid kuna investeerisite riskivabadesse võlakirjadesse peaaegu kogu aasta, oleks teie portfelli variatsioon (ja standardhälve) peaaegu null – andes teile äärmiselt kõrge Sharpe’i suhte, mis võib olla suurem kui 10!

Teine investor valis väga stabiilsed indeksifondid, mille aastane tootlus oli 10%. Kuid kuna hind tõusis ja langes iga päev veidi, oli seal mõningane variatsioon, seega võib nende Sharpe’i suhe olla vaid umbes 3 – tavaliselt peetakse seda suurepäraseks. Kui võrrelda ainult Sharpe’i suhet, näeb teie Sharpe’i suhe 10 suurepärane välja, kuid tegelikult tegi teine investor tõenäoliselt targema investeerimisotsuse.