Diskreční výdaje – Pochopení centrální tendence
Co jsou diskreční výdaje?
Diskreční výdaje jsou nepodstatné nákupy – přání, věci, které kupujeme pro potěšení, pohodlí nebo zábavu. Příklady zahrnují zábavu, stravování mimo domov nebo nejnovější technologické gadgety. Naopak potřeby jsou nezbytné pro přežití: jídlo, bydlení, služby a zdravotní péče. Znalost rozdílu mezi potřebami a přáními je klíčová finanční dovednost, zejména když začnete spravovat své vlastní peníze.

Proč je to důležité
Pochopení rozdílu mezi potřebami a přáními vám pomáhá činit chytřejší finanční rozhodnutí. Například, pokud jste si našetřili na novou videohru, ale váš telefon se rozbije, co si vyberete? Telefon je potřeba; hra je přání. Rozhodnutí nahradit telefon zajišťuje, že splníte nezbytný výdaj, což vás připraví na finanční bezpečnost v dlouhodobém horizontu.
Analýza potřeb vs. přání: Datový přístup
Sledování vašich výdajů pomáhá odhalit vzorce ve vašich finančních návycích. Můžete sledovat, kolik vy a vaši přátelé utrácíte za nepodstatné položky, jako jsou svačiny, zábava nebo aplikace. Zkoumáním těchto dat můžete přemýšlet o tom, zda vaše výdaje odpovídají vašim prioritám.
Ve skutečnosti výzkum ukazuje, že lidé, kteří myslí dlouhodobě, mají tendenci šetřit více, zatímco ti, kteří se soustředí na okamžité uspokojení, mají větší pravděpodobnost, že přečerpají. Analýza vašich výdajových dat vám může pomoci činit lepší finanční rozhodnutí a budovat zdravější finanční návyky.
Použití centrální tendence k analýze výdajových dat
Při analýze výdajů tři klíčové míry centrální tendence – průměr, medián a modus – pomáhají shrnout vaše finanční chování:
- Průměr: Průměr všech vašich výdajů. I když je užitečný, průměr může být zkreslen extrémními hodnotami (například někdo utrácí mnohem více nebo méně než ostatní).
- Medián: Střední hodnota, když jsou všechna data seřazena. To dává lepší představu o typických výdajích tím, že se vyhýbá odlehlým hodnotám.
- Modus: Nejčastější hodnota. To může pomoci identifikovat běžné návyky nebo populární trendy ve výdajích.
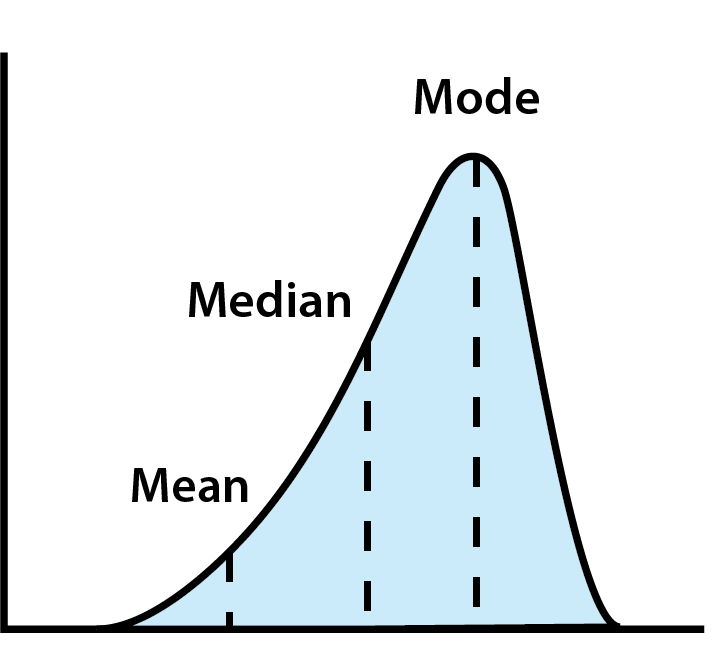
Použití centrální tendence k analýze výdajových dat
Pohled na centrální tendenci může pomoci uvést váš vlastní rozpočet do perspektivy. Například si můžete každý den ráno koupit kávu na cestě do školy nebo do práce. Uvědomujete si, že to může být hodně, ale myslíte si, že utrácíte přibližně stejně jako ostatní, takže je to rozumný výdaj.
Ale pokud se skutečně zeptáte skupiny svých vrstevníků, kolik utrácejí, může vám to poskytnout širší perspektivu o tom, kolik vlastně utrácíte každý měsíc.
- Průměr: Pokud zjistíte, že utrácíte přibližně stejně jako průměr, pak jste měli pravdu o svých vlastních výdajových návycích. Ale pokud zjistíte, že utrácíte mnohem více než ostatní, možná se podíváte blíže na své nápoje.
- Medián: Medián vám říká, jak vaše jednání zapadá do ostatních. Možná několik lidí utratí $0 za kávu – to by zkreslilo průměr níže, než co typický konzument kávy utrácí. V tomto případě byste mohli vidět, že vlastně utrácíte méně než medián, takže vaše výdaje jsou skutečně rozumné.
- Modus: Nejčastější hodnota. Možná skupina přátel si každý den ráno objednává stejný Orange Mocha Frappuccino – což z něj dělá módní volbu. Pokud víte, že Orange Mocha Frappuccino je drahé, může to znamenat, že medián je také zkreslen výše, než co si myslíte, že typický konzument kávy objednává.
Příklad: Estebanův kávový zvyk
Esteban si každý den ráno kupuje kávu za $4.75. I když věří, že to je rozumná cena, zajímá ho, zda je to typické. Aby získal lepší představu o průměrné ceně, ptá se svých přátel, rodiny a kolegů, kolik utratili za svou ranní kávu. Toto jsou jejich odpovědi:

| Respondent | Kolik utratili dnes ráno |
|---|---|
| 1 | $0.00 |
| 2 | $6.95 |
| 3 | $1.99 |
| 4 | $0.00 |
| 5 | $4.25 |
| 6 | $3.00 |
| 7 | $5.99 |
| 8 | $7.37 |
| 9 | $0.00 |
| 10 | $8.19 |
| 11 | $7.59 |
| 12 | $0.00 |
| 13 | $24.68 |
| 14 | $0.00 |
| 15 | $8.09 |
1. Výpočet průměru
Nejprve chce Esteban otestovat svou první hypotézu – že utrácí přibližně průměrně jako ostatní. Takže by vypočítal průměr, nebo střední hodnotu. Vzorec pro výpočet průměru je:
Průměr = součet pozorování / počet pozorování
Vzorec lze také napsat v tom, co se nazývá Sigma Notace:
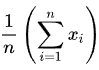
V Sigma Notaci znamená znak Sigma (Σ) “sečíst”, znak n znamená kolik pozorování, x znamená pro konkrétní pozorování, a i znamená pro každé pozorování. Takže to, co to říká, je, že od prvního (i = 1, na spodní části sigma) po poslední pozorování (k n, které je nahoře sigma), sečtěte všechny jejich hodnoty, a pak vynásobte 1/n. Sigma Notace je velmi běžná v oblasti výzkumu, protože ukazuje algebraické nebo matematické operace aplikované na celou řadu čísel, místo jednoho po druhém.
Takže sečteme všechna pozorování:
$0.00 + $6.95 + $1.99 + $0.00 + $4.25 + $3.00 + $5.99 + $7.37 + $0.00 + $8.19 + $7.59 + $0.00 + $24.68 + $0.00 + $8.09 = $78.10
A vydělíme 15 (počet pozorování)
$78.10 / 15 = $5.21
Esteban měl pravdu – utrácí méně než průměr. Jeho $4.75 je levnější než průměrná hodnota $5.21.
2. Výpočet mediánu
Abychom vypočítali medián, musíme seřadit hodnoty od nejmenší po největší. Medián je střední číslo.
| Respondent | Kolik utratili dnes ráno |
|---|---|
| 1 | $0.00 |
| 4 | $0.00 |
| 9 | $0.00 |
| 12 | $0.00 |
| 14 | $0.00 |
| 3 | $1.99 |
| 6 | $3.00 |
| 5 | $4.25 |
| 7 | $5.99 |
| 2 | $6.95 |
| 8 | $7.37 |
| 11 | $7.59 |
| 15 | $8.09 |
| 10 | $8.19 |
| 13 | $24.68 |
Střední hodnota (medián) výdajů jeho přátel, rodiny a kolegů na ranní kávu je ve skutečnosti $3.00, což je výrazně méně než Estebanových $4.75. Tento objev dělá Estebana méně pohodlným ohledně jeho každodenní kávy. Uvědomuje si, že utrácí o 50 % více než jeho vrstevníci, i když jeho individuální náklady jsou pod průměrnou cenou.
3. Výpočet módu
Na závěr chce Esteban zjistit, jaká je nejoblíbenější volba. K tomu potřebuje najít mód. Mód je jednoduše nejběžnější pozorování. V případě jeho průzkumu odpovědělo 5 lidí $0.00 – což činí tuto volbu nejoblíbenější (mód). I když to není většina lidí, má to určitě velký dopad na průměr a medián. Esteban si není úplně jistý, co s těmito informacemi dělat – ale existuje více matematiky, která mu pomůže najít odpověď!
Interpretace dat: Skewness, odlehlé hodnoty a rozdělení
Esteban se dívá na problémy ve své analýze vyplývající z rozložení jeho odpovědí – nebo jak jeho odpovědi vypadají na grafu.
Šikmost
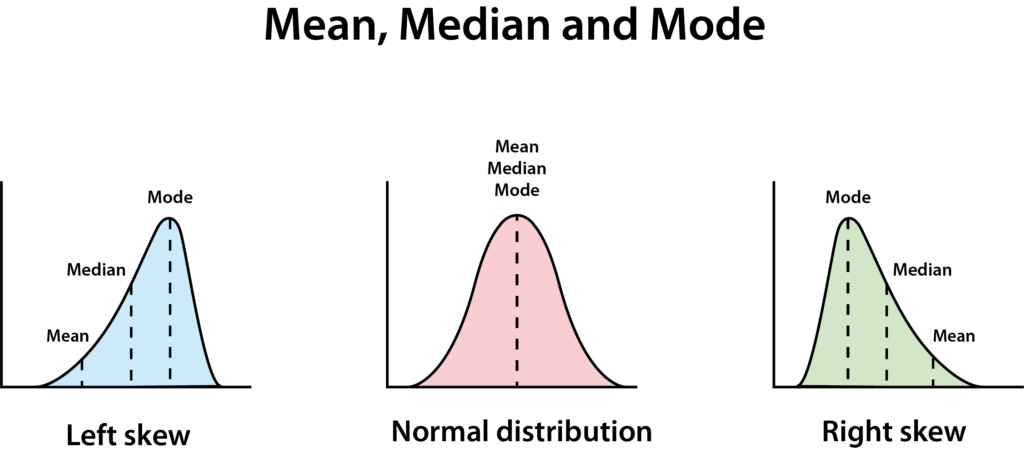
Normální rozložení má čistý tvar zvonu. Perfektně normální rozložení znamená, že průměr, medián a modus jsou si rovny.
Pokud nejsou všechny rovny, znamená to, že data jsou šikmá – v tomto případě říkáme, že jeho data mají pravou šikmost, což znamená, že medián je nižší než průměr. K tomu často dochází, když je málo opravdu velkých nebo opravdu malých čísel, což způsobuje, že graf vypadá, jako by měl dlouhý skluz směrem doprava.
Odlehlé hodnoty
Když Esteban pečlivě zkoumá odpovědi, všimne si jedné odlehlé hodnoty: náklad ve výši 24,68 $. Tato hodnota je výrazně vyšší než jakákoli jiná. Odlehlé hodnoty jsou datové body, které jsou daleko od zbytku skupiny a často jsou vyloučeny ze statistické analýzy, protože mohou zkreslit výsledky.
Po dalším vyšetřování se Esteban dozvídá, že tato odlehlá hodnota představuje náklady na galon čerstvě vymačkané pomerančové šťávy zakoupené pro celou rodinu dané osoby toho rána. Tento výdaj se jasně nedá srovnávat s typickými náklady na jeden šálek kávy.
Bimodální rozložení
Bimodální rozložení nastává, když se podíváte na frekvenční rozložení a nevidíte pouze jeden vrchol, ale dva (nebo více). Podívejte se na tyto odpovědi z průzkumu, kolik studenti středních škol zaplatili za obědy v daný den:
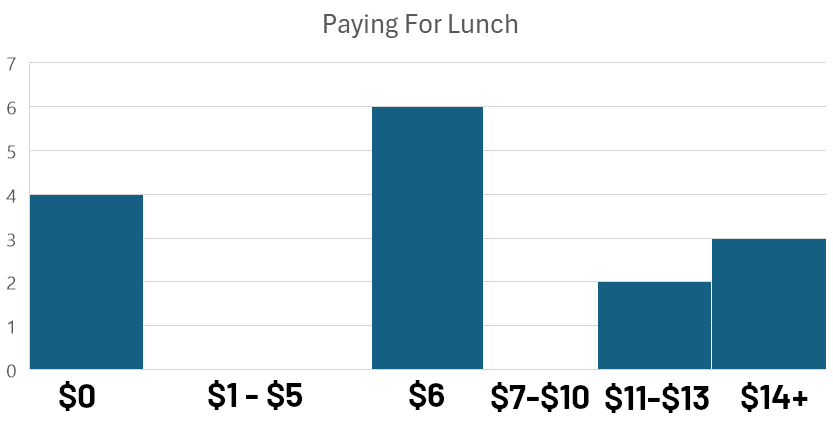
Tento typ grafu, kde jsou data seskupena do intervalů nebo ‘binů’ pro vizuální srovnání, se nazývá histogram. Analýza toho, jak jsou pozorování rozdělena v těchto binech, se nazývá frekvenční analýza.
Při pozorování histogramu si všimneme dvou výrazných vrcholů: jednoho blízko 0 $ a druhého blízko 6 $. Toto bimodální rozložení (s módy blízko 0 $ a 6 $) naznačuje, že v datech existují dvě odlišné skupiny.
Identifikace těchto vrcholů může vést k dalšímu výzkumu tím, že vyvolá otázky, jako jsou:
- Jaké faktory by mohly vysvětlit tyto dva odlišné vzorce výdajů?
- Co tyto vrcholy odhalují o základních motivacích a chování jednotlivců v těchto skupinách?
Navíc přítomnost těchto dvou vrcholů naznačuje pravou šikmost, což znamená, že větší podíl datových bodů je shromážděn směrem k dolnímu konci cenového spektra.
Bimodální data neznamenají nutně, že existují dvě odpovědi se stejným počtem pozorování, jen to, že vidíme dva jasné vrcholy (v tomto případě je 6 $ “skutečný mód”).
Když se výzkumníci podívali blíže na data, vysvětlení se stalo zřejmým. 0 $ byli studenti, kteří si přinesli oběd z domova, a 6 $ byly náklady na běžný školní oběd. Studenti, kteří zaplatili více než 10 $, si kupovali kombinaci položek z školního bufetu a další potraviny, které si koupili na cestě do školy.

Závěr: Používání dat k lepším finančním rozhodnutím
Porozuměním těmto třem měřením centrální tendence: průměr, medián a modus můžete interpretovat data a činit informovanější finanční rozhodnutí. Ať už analyzujete své výdaje nebo se díváte na větší trendy, tyto nástroje vám umožňují rozvíjet lepší finanční návyky. Shromažďování a analýza dat o výdajích může poskytnout vhled do vašeho finančního chování.
Pro studenty jako Esteban mohou jednoduché změny – jako snížení výdajů na volitelné položky – vést k dlouhodobým finančním výhodám. Když Esteban vidí, že jeho výdaje jsou nad mediánem – a že nejoblíbenější volbou je vůbec neutrácet, pomáhá mu to dát do kontextu jeho rozhodnutí o výdajích a co to znamená pro jeho budoucnost.