9-08 Oceňování opcí – Model Black-Scholes
Jakákoli diskuse o opcích a cenách opcí by byla neúplná bez zmínky o Black-Scholes modelu oceňování opcí.
Akademici Fischer Black a Myron Scholes ve své práci z roku 1973 uvedli svou teorii, že opce byla implicitní součástí oceňování jakéhokoli obchodovaného cenného papíru.
Odkazujíc na práci některých z nejznámějších ekonomů, jako je Paul Samuelson, Black a Scholes vyvinuli nikoli jednu, ale tři “pozice” k vašemu zvážení.
- Model Black-Scholes: Matematický výpočet týkající se akcií (cenných papírů).
- Black-Scholes PDE (parciální diferenciální rovnice): Tato rovnice sleduje pohyb určité akcie.
- Black-Scholes vzorec: Tento vzorec se pokouší vypočítat ceny pro put a call opce .
Pokud nejste oddaný a beznadějný matematik, potřebujete pouze vědět, jak může práce Black-Scholes ovlivnit vaše investiční aktivity. Zatímco mnozí odborníci uvádějí omezení této teorie, můžete přijmout předpovědi a projekce nabízené výpočty Black-Scholes, abyste podpořili svou činnost s opcemi.
Black-Scholes vzorec se používá k získání ceny evropských put a call opcí. Je získán řešením Black–Scholes PDE – viz odvození níže.
Pomocí tohoto vzorce je hodnota call opce z hlediska parametrů Black–Scholes:
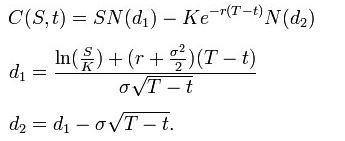
Cena put opce je:
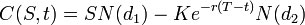
Pro obě, jak je uvedeno výše:
- N(•) je kumulativní distribuční funkce standardního normálního rozdělení
- T – t je doba do splatnosti
- S je spotová cena podkladového aktiva
- K je strike price
- r je bezriziková sazba (roční sazba, vyjádřená v termínech kontinuálního úročení)
- σ je volatilita v logaritmických výnosech podkladového aktiva

