复利
复利是现代世界中最重要的概念之一,也是每个经济体金融系统的基石。“复利”的概念出奇简单,但却极其强大!
单利
在我们讨论复利的力量之前,我们首先需要了解单利。
在金融世界中,单利是贷款的回报。例如,如果你的朋友借你100美元,并承诺一年后还你110美元,那么你通过借出这笔钱将赚取10美元的利润。“利息”是回报率,或者说你赚取的利润占原始投资的百分比。在投资术语中,你投资的原始100美元被称为“本金”。

利息 = (还款 – 本金) / 本金
在上面的例子中,赚取的利息是10%。
(110 – 100) / 100 = 10%
在金融世界中,利息通常以每年的回报来表示。如果你的朋友承诺在6个月内还款,那么“年利率”将会调整。由于6个月是1年的一半,因此“年利率”是6个月回报的两倍。
年利息 = 利息 * 贷款期限,作为1年的百分比
因此,如果朋友在6个月内还款,年利息将是20%。
年利息 = 10% * 2 = 20%
因此,在20%回报(你的朋友在6个月内还款,加上10美元)和10%回报(朋友等待12个月还款)之间选择,20%回报显然更好。
单利与债券
债券投资是通过单利运作的。债券通常价格为1000美元,每个债券都有一个利率和到期日(通常是发行后30年)。
如果你购买一张1000美元的债券,这张债券每年将支付50美元,持续30年。在第30年结束时,你将获得最后的50美元支付,加上你原始的1000美元本金——每年简单的5%利息支付。

单利与复利
单利就是这样——简单。复利在表面上稍微复杂一些。使用复利时,不仅仅是在贷款结束时支付利息,而是“还款”金额被重新投资。
让我们回想一下朋友借100美元的例子。当他在1年后还款时,正当他递给我们110美元时,他请求再借110美元一年,并支付同样的10%利息。这意味着在下一年结束时,他的“利息支付”将是110美元 * 10% = 11美元,因此他总共还款的金额将是121美元。
因为朋友借的是全部金额——包括第一年的利息,回报更大!这意味着每年,每笔贷款的“还款”都会加到原始贷款金额上,“复利”本金(和赚取的利息)到下一年。
复利的例子
复利通常用于储蓄和投资。储蓄账户是复利的经典例子。你的银行每月会对你的储蓄支付利息——而这些利息会存入储蓄账户本身。这意味着下个月,它将对原始存款和第一个月赚取的利息都赚取利息。
在股市投资也被视为一种复利形式。如果投资的价值每年上涨10%,这意味着前一年的回报被包含在收益中!
72法则
72法则是一种简单的方法,用于估算你的投资在复利下需要多长时间才能翻倍。你只需将72除以年利率(以百分比形式)——这会告诉你原始投资翻倍所需的确切时间!
| 利率 | 翻倍时间 |
|---|---|
| 1% | 72年 |
| 2% | 36年 |
| 5% | 14.4年 |
| 10% | 7.2年 |
| 20% | 3.6年 |
复利与单利 – 实践中
现在我们已经看到了单利(通过债券)和复利(通过储蓄账户)的运作方式。但为了看到复利为何如此强大,让我们来看一个30年的比较(债券的平均到期时间),以查看我们两项投资之间的回报差异。
单利
| 年份 | 本金 | 赚取的利息 |
| 1 | $ 1,000 | $50 |
| 2 | $ 1,000 | $50 |
| 3 | $ 1,000 | $50 |
| 4 | $ 1,000 | $50 |
| 5 | $ 1,000 | $50 |
| 6 | $ 1,000 | $50 |
| 7 | $ 1,000 | $50 |
| 8 | $ 1,000 | $50 |
| 9 | $ 1,000 | $50 |
| 10 | $ 1,000 | $50 |
| 11 | $ 1,000 | $50 |
| 12 | $ 1,000 | $50 |
| 13 | $ 1,000 | $50 |
| 14 | $ 1,000 | $50 |
| 15 | $ 1,000 | $50 |
| 16 | $ 1,000 | $50 |
| 17 | $ 1,000 | $50 |
| 18 | $ 1,000 | $50 |
| 19 | $ 1,000 | $50 |
| 20 | $ 1,000 | $50 |
| 21 | $ 1,000 | $50 |
| 22 | $ 1,000 | $50 |
| 23 | $ 1,000 | $50 |
| 24 | $ 1,000 | $50 |
| 25 | $ 1,000 | $50 |
| 26 | $ 1,000 | $50 |
| 27 | $ 1,000 | $50 |
| 28 | $ 1,000 | $50 |
| 29 | $ 1,000 | $50 |
| 30 | $ 1,000 | $50 |
| 总计 | $1,500 |
复利
| 年份 | 本金 | 赚取的利息 |
| 1 | $ 1,000 | $ 50 |
| 2 | $ 1,050 | $ 53 |
| 3 | $ 1,103 | $ 55 |
| 4 | $ 1,158 | $ 58 |
| 5 | $ 1,216 | $ 61 |
| 6 | $ 1,276 | $ 64 |
| 7 | $ 1,340 | $ 67 |
| 8 | $ 1,407 | $ 70 |
| 9 | $ 1,477 | $ 74 |
| 10 | $ 1,551 | $ 78 |
| 11 | $ 1,629 | $ 81 |
| 12 | $ 1,710 | $ 86 |
| 13 | $ 1,796 | $ 90 |
| 14 | $ 1,886 | $ 94 |
| 15 | $ 1,980 | $ 99 |
| 16 | $ 2,079 | $ 104 |
| 17 | $ 2,183 | $ 109 |
| 18 | $ 2,292 | $ 115 |
| 19 | $ 2,407 | $ 120 |
| 20 | $ 2,527 | $ 126 |
| 21 | $ 2,653 | $ 133 |
| 22 | $ 2,786 | $ 139 |
| 23 | $ 2,925 | $ 146 |
| 24 | $ 3,072 | $ 154 |
| 25 | $ 3,225 | $ 161 |
| 26 | $ 3,386 | $ 169 |
| 27 | $ 3,556 | $ 178 |
| 28 | $ 3,733 | $ 187 |
| 29 | $ 3,920 | $ 196 |
| 30 | $ 4,116 | $ 206 |
| 总计 | $3,322 |
在这个例子中,你可以看到复利的总回报是单利的两倍以上——这很强大!如果你查看投资的总价值图表,你也可以看到形状上的明显差异:
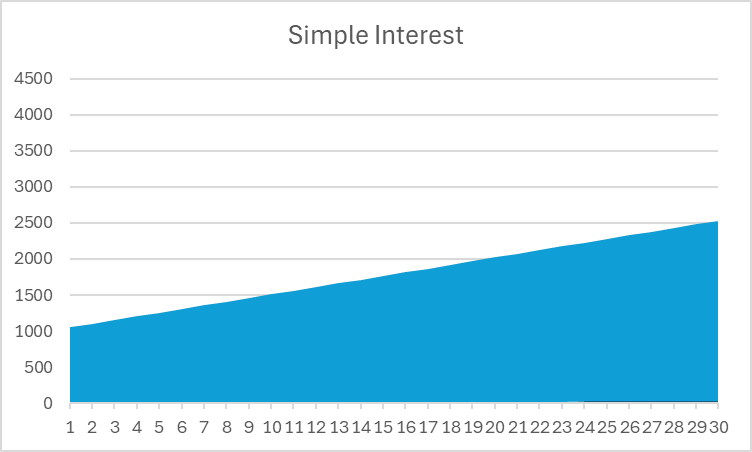
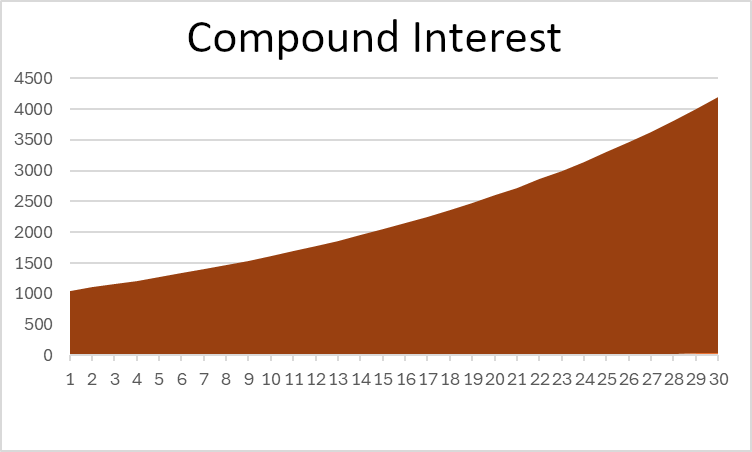
注意,单利是一条直线,而复利随着时间的推移向上弯曲。
单利的案例
尽管你肯定希望你的储蓄随着时间的推移而复利,以获得更好的长期回报,但这并不意味着单利应该被忽视。这只是意味着如果你希望储蓄复利,你需要做更多的工作。
以投资债券为例。虽然债券支付单利,但你可以将这些支付再投资到其他地方(例如存入储蓄账户或购买更多债券)——即使它是单利,也能给自己带来“复利回报”。
只要你继续再投资你的回报(而不是花掉或持有现金),你就总是在复利!
复利频率
复利还有一个最后的考虑因素,这可能会使事情变得更加复杂——复利频率。
我们之前提到过,储蓄账户每月支付利息——尽管它使用的是5%的年利率。这意味着你的银行实际上每月支付5% / 12的利息(或大约0.42%)。
这意味着你的银行账户以较低的利率但更高的频率进行复利,而另一家银行账户则只按年支付利息。因为你的账户更频繁地复利,这意味着你的“有效”回报稍微高一些——以5%的利率和$1,000的储蓄,复利一次将产生$1,050,但每月复利的结果约为$1051.16。那额外的$1.16并不多——但也不是没有。

复利公式
得益于指数的力量,我们可以计算复利投资的最终余额,而无需像上面那样手动计算每一年。公式是:
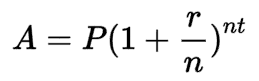
其中:
- A 是最终余额
- P 是起始本金
- r 是利率(在金融中,通常是年利率)
- n 是投资复利的周期数
- 而 t 是我们测量的时间周期数。
在我们30年年复利的例子中,P 将是$1,000,r 将是5%,n 将是1(每年复利一次),而t 将是30,表示30年。如果我们计算月利息,“n”将是12,因为它每年复利12次。
您可以通过使用我们的复利计算器来查看不同类型的复利和不同利率之间的差异!
Return To Glossary