الحدود والسجلات – الإنفاق والتوفير الشخصي
تركز معظم الأمور المالية الشخصية على التفكير على المدى الطويل: بناء ميزانيتك حتى تتمكن من ادخار ما يكفي من المال لتعيش نمط الحياة الذي تريده، والتقاعد بشكل مريح.
لكن بالنسبة لكل فرد، يمكن أن تعني “نمط الحياة الذي تريده” و”التقاعد بشكل مريح” أشياء مختلفة تمامًا. في نهاية المطاف، يتخذ كل شخص قرارًا كل شهر يعمل فيه حول مقدار ما سينفقه (أو يستهلكه) ومقدار ما سيوفره (أو يستثمره).
من خلال فهم عملية التفكير وراء هذا التبادل، يمكنك الحصول على صورة أوضح عن إنفاقك الخاص. سيساعدك ذلك في التأكد من أن إنفاقك الفعلي يتطابق مع إنفاقك المقصود.
نمذجة الاستهلاك – العوائد المتناقصة على المقياس
تركز معظم الرياضيات المالية على النمو الأسي – كيف ينمو الاستثمار بناءً على معدل الفائدة، كيف ينمو حساب التوفير مع مرور الوقت، أو كيفية بناء الثروة على المدى الطويل. تحتوي الدوال الأسية على منحنى صاعد – تزداد الاستثمارات مع مرور الوقت:

لكن عندما تنفق بدلاً من الادخار، فإن الفائدة التي تحصل عليها مقابل كل دولار تنفقه لا تحتوي على ذلك المنحنى الصاعد. بدلاً من ذلك، يقول الاقتصاديون إن الاستهلاك له عوائد متناقصة على المقياس.
فكر في الأمر بهذه الطريقة – ترى شقتين للإيجار. واحدة تحتوي على غرفة نوم واحدة، والأجهزة عمرها 30 عامًا، والحمام صغير، والمطبخ ليس لديه حتى مساحة لطاولة. هذه الشقة مدرجة للإيجار بمبلغ 500 دولار / شهر.
الشقة الثانية تحتوي على أجهزة جديدة تمامًا، وحمام واسع مع حوض استحمام ودش منفصل، والمطبخ يحتوي على أسطح جرانيت مع مساحة لطاولة وبار إفطار. هذه مدرجة للإيجار بمبلغ 1500 دولار / شهر.
الآن قد تكون الشقة الثانية تستحق بالفعل 1000 دولار أكثر في الشهر. لكن القيمة التي تحصل عليها من وجود شقة (مكان للنوم ليلاً، تخزين ممتلكاتك بأمان، طهي وطعام، إلخ) هي الجزء الأكثر أهمية. إذا حاولت تقسيم جميع المرافق المختلفة التي تحصل عليها مع الشقة الأكثر تكلفة لرؤية مصدر كل القيمة، فقد يبدو الأمر هكذا:
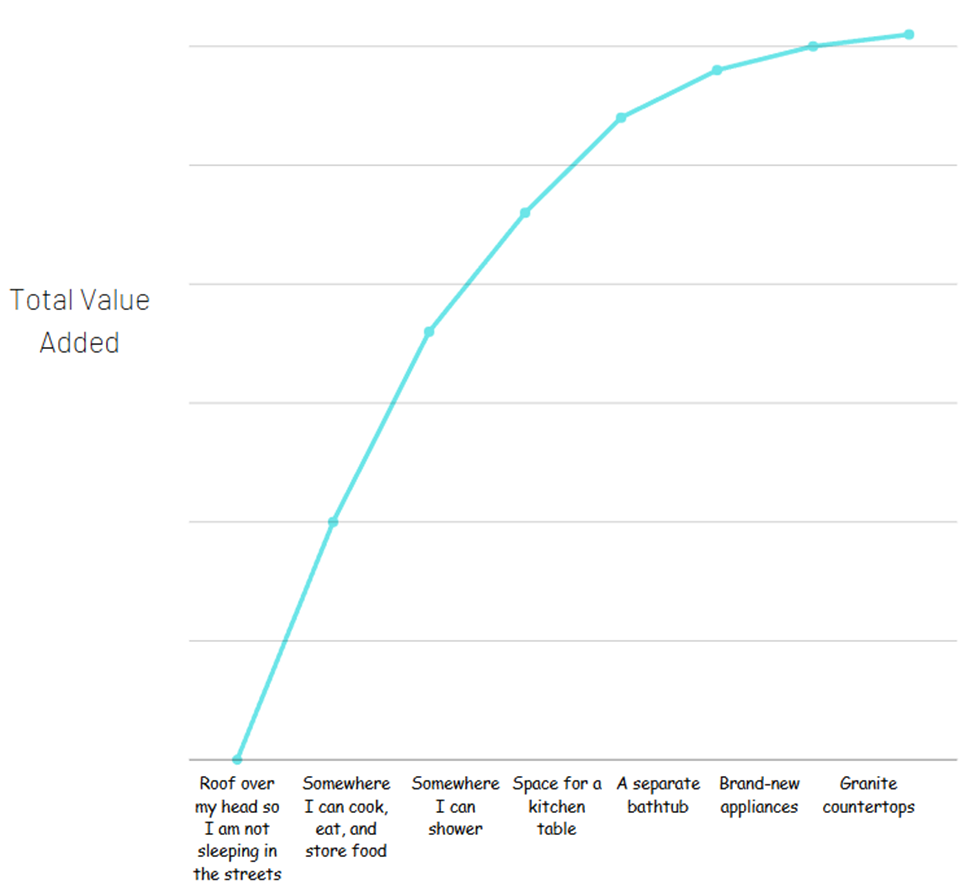
تأتي معظم القيمة الإجمالية من أساسيات الأساسيات. وهذا لا يعني بأي شكل من الأشكال أن الإضافات ليست ذات قيمة – لا توجد علامات دولار هنا، فقط مقدار القيمة التي تحصل عليها.
في الاقتصاد، يُطلق على هذا المفهوم اسم المنفعة – الرضا أو الفائدة المستمدة من استهلاك السلع أو الخدمات. ستلاحظ أن المنحنى يتسطح مع زيادة الإنفاق. لنمذجة ذلك رياضيًا، نستخدم اللوغاريتمات بدلاً من الأسس.
ما هو اللوغاريتم؟
يمكنك التفكير في اللوغاريتمات بالنسبة للأسس بنفس الطريقة التي ترتبط بها القسمة بالضرب – إنها الوظيفة الرياضية المعاكسة. بعبارة أخرى،
إذا كان 2^3 = 8، فإن 3 هو اللوغاريتم لـ 8 على أساس 2.
في الاقتصاد والمالية، تكون اللوغاريتمات مفيدة لإظهار هذه العوائد المتناقصة على المقياس للإنفاق. على سبيل المثال، إذا أردنا عمل رسم بياني يظهر المنفعة المستلمة من الاستهلاك خلال شهر معين، قد يبدو الرسم البياني هكذا:
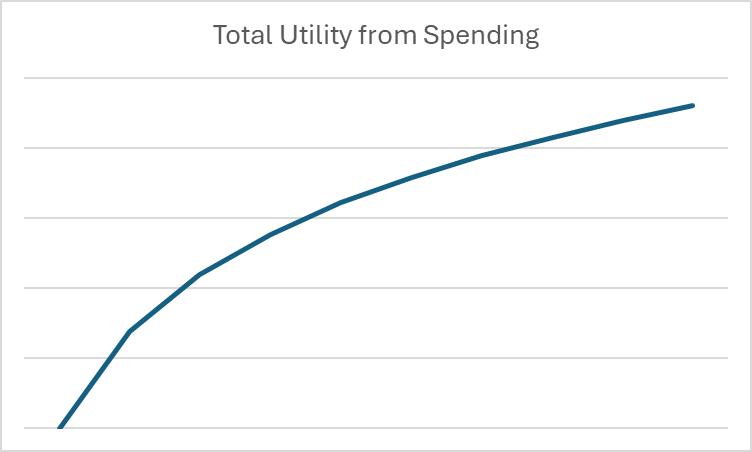
بمجرد أن نضع إنفاقنا في سياق اللوغاريتمات والمنفعة، يمكننا البدء في النظر إلى قرارات الإنفاق والتوفير على المدى الطويل بشكل رياضي بحت.
قيمة الوقت للمال – معدلات الخصم
تشير قيمة الوقت للمال إلى حقيقة أن الدولار في المستقبل يساوي أقل من دولار اليوم. وذلك لأنه بين الآن والمستقبل، كان بإمكاني استخدام ذلك الدولار للقيام بشيء ما – وقد تكون تلك الفرصة قد فاتت.
عندما نريد وصف قيمة الوقت للمال رياضيًا، نستخدم شيئًا يسمى معدل الخصم. معدل الخصم هو رقم بسيط بين 0 و 1 يجيب على هذا السؤال:
كم ستتنازل اليوم للحصول على 1 دولار بعد شهر؟

معدل الخصم لكل شخص مختلف – يشير إلى مدى قصر أو طول تفضيلاتهم الشخصية. كما قد تتوقع، فإن الشخص الذي لديه معدل خصم مرتفع (على سبيل المثال، 0.9) من المرجح أن يكون مدخرًا أكثر من شخص لديه معدل خصم منخفض (على سبيل المثال، 0.3). وذلك لأن الشخص الذي لديه معدل خصم منخفض يقدر كثيرًا الحصول على ذلك المال الآن – لذا فهو مستعد للتنازل عن 70% من قيمته للحصول عليه على الفور بدلاً من الانتظار.
عادة ما يتم التعبير عن معدل الخصم باستخدام الحرف اليوناني β. لذا إذا كان معدل خصمك الشخصي هو 0.95، سنقول β = 0.95.
معدلات الخصم والأسس
بمجرد أن تتمكن من تحديد معدل الخصم الشخصي الخاص بك، يمكنك أيضًا استخدام ذلك لمعرفة كم ستأخذ مقابل ذلك الدولار إذا كان أبعد في المستقبل باستخدام الأسس.
من خلال رفع بيتا الخاص بك إلى أس يساوي مدى بُعد الوقت الذي نريد حسابه، يمكننا أن نقول كم يساوي ذلك الدولار اليوم. بعبارة أخرى، β ^t = كم ستكون مستعدًا لأخذه اليوم مقابل دولار t شهور من الآن.
في مثالنا حيث β = 0.95، هذه هي قيمة الدولار على مدار السنة القادمة:
| الشهور في المستقبل | كم ستكون مستعدًا لأخذه اليوم للتضحية بدولار في المستقبل |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
هذا يعني أنه إذا كانت β = 0.95، ستكون مستعدًا لأخذ 0.54 دولار للتضحية بدولار بعد عام من الآن.
الآن بعد أن لدينا مفهوم كل من اللوغاريتمات ومعدلات الخصم، يمكننا تجميعها لنرى ماذا يعني ذلك لقرارات الادخار والإنفاق على المدى الطويل!
المنفعة مدى الحياة
معظم ما تتعلمه في فصل التمويل الشخصي يتعلق بالادخار للمستقبل، وخاصة التقاعد. لكن هذا ليس حقًا هدفك المالي في الحياة – أنت تريد حقًا تعظيم منفعتك الإجمالية مدى الحياة. لهذا السبب لا يوفر أحد كل قرش – أنت توازن بين منفعتك (أو المنفعة) من الإنفاق اليوم وبين زيادة ثروتك (من خلال قوة الفائدة المركبة) حتى تتمكن من إنفاقها في المستقبل.
هذا يعني أنه في كل شهر من حياتك، لديك دخلك لذلك الشهر، بالإضافة إلى جميع المدخرات التي قمت بتجميعها حتى ذلك الحين. هذه الموارد المجمعة هي ما لديك لتعمل به. أنت تقرر بوعي كم من هذه الموارد ستنفق (أو تستهلك) وكم ستوفر (أو تستثمر). لديك أيضًا بعض الفهم لمعدل الفائدة الذي ستنمو به مدخراتك بمرور الوقت. من الناحية الرياضية، أنت تختار c و i حيث:
I + (s x (1 + r)) = c + i
حيث تشير هذه المتغيرات إلى:
- I = دخلك هذا الشهر
- s = كم لديك بالفعل من المدخرات/الاستثمارات في بداية الشهر
- r = معدل الفائدة الذي تنمو به مدخراتك. لذا ستنمو مدخراتك من الشهر الماضي قليلاً بحلول بداية هذا الشهر مقارنة بما كان لديك في الشهر الماضي.
- c = كم تستهلك/تنفق هذا الشهر
- i = كم توفر/تستثمر هذا الشهر
يمكن التعبير عن المنفعة التي تحصل عليها من الاستهلاك من خلال أخذ لوغاريتم استهلاكك:
المنفعة = log(c)
تحتاج إلى تحديد مقدار ما ستنفقه (وبالتالي توفره) في كل فترة لتعظيم منفعتك الإجمالية مدى الحياة، وليس فقط سعادتك في اللحظة الحالية. باستخدام معدل الخصم والأسس، يمكننا حساب المنفعة التي ستحصل عليها من الاستهلاك في أي فترة في المستقبل، ثم نجمعها جميعًا.
إجمالي المنفعة مدى الحياة =
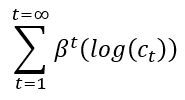
الحدود – نهج المنفعة والخصومات تقترب من الصفر
في البداية، يبدو أن هذا قد يكون لانهائيًا – نحن نجمع أعدادًا لانهائية، لذا قد يصبح أكبر وأكبر إلى الأبد. ومع ذلك، لأن t يستمر في النمو، فهذا يعني أن الخصم المطبق في المستقبل البعيد يبدأ في الاقتراب جدًا من الصفر.
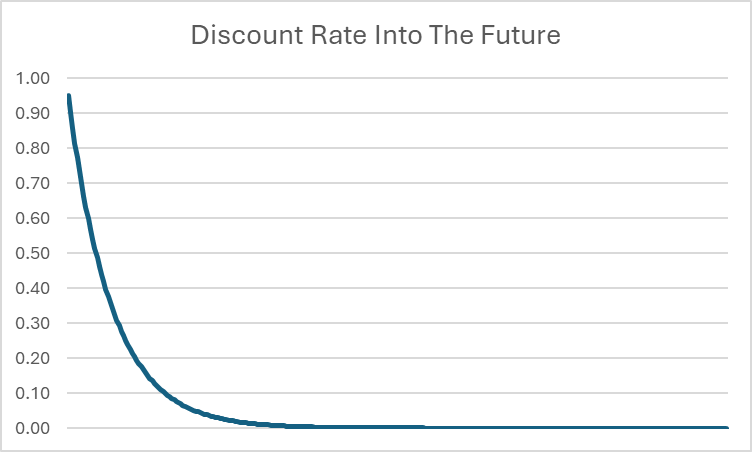
على سبيل المثال، حتى إذا كان β = 0.95، فإن معدل الخصم بعد 20 عامًا ينخفض إلى 0.0000045. كلما ابتعدنا في المستقبل، كلما اقترب معدل الخصم من 0. بينما قد يكون من المستحيل حساب الحد الأقصى الدقيق لاستهلاك الحياة بدقة مطلقة (حيث قد يتطلب نظريًا عددًا لانهائيًا من الأماكن العشرية)، يمكننا أن نقول بثقة أنه يوجد حد أعلى لمجموع الاستهلاك القابل للتحقيق على مدى الحياة.
تستخدم الحدود لتعريف تلك الحدود العليا والسفلى. يمكننا أن نقول بأمان أن معدل الخصم له حد أدنى قدره 0 حيث يستمر t في النمو إلى اللانهاية – سيستمر في الاقتراب من 0، لكنه لن يصل إليه أبدًا. يمكن أيضًا حساب الحد الأعلى للمنفعة الكلية على مدى الحياة (لكن القيام بذلك يتطلب بعض حساب التفاضل المتقدم، وهو ليس جزءًا من هذا الدرس).
معدلات الخصم ومعدلات الفائدة – اختيار الادخار
بمجرد أن نتجاوز كل الرياضيات، ما يمكننا رؤيته حقًا هو أن قرار الإنفاق أو الادخار يعتمد حقًا على متغيرين فقط:
- معدل الخصم الشخصي الخاص بك (أو β)
- معدل الفائدة r، الذي يحدد مدى نمو استثماراتك
إذا كان هناك شخصان يتوقعان نفس العائد على الاستثمار لمدخراتهما، لكننا نلاحظ أن شخصًا ما هو مدخر كبير والآخر هو منفق كبير، يمكننا أن نقول إن المدخر لديه β أعلى من المنفق – يمكننا استخدام رقم فعلي لتحديد مدى كون شخص ما مدخرًا أو منفقًا.

فهم قوي لمعدلات الفائدة أمر حاسم للمعرفة المالية. إذا كانت خيارك الوحيد للادخار هو حساب توفير منخفض الفائدة (ربما يكسب فقط 3% سنويًا)، فمن غير المرجح أن تعطي الأولوية لأهداف الادخار على المدى الطويل. وذلك لأنك قد لا تدرك تمامًا إمكانيات الاستثمارات ذات المخاطر العالية والعوائد العالية مثل سوق الأسهم.
في النهاية، الجانب الأكثر أهمية في المعرفة المالية هو أن تكون على دراية بخيارات الاستثمار المتاحة لك واتخاذ قرارات مستنيرة بناءً على ظروفك الفردية وتحمل المخاطر.