9-08 Valoración de opciones: modelo Black-Scholes
Cualquier análisis de opciones y precios de opciones estaría incompleto sin mencionar el modelo de valoración de opciones más aceptado, el modelo Black-Scholes.
Los académicos Fischer Black y Myron Scholes, en un artículo de 1973, expusieron su teoría de que una opción estaba implícita en la valoración de cualquier valor negociado.
Refiriéndose al trabajo de algunos de los economistas más famosos, como Paul Samuelson, Black y Scholes desarrollaron no una, sino tres “posiciones” para su consideración.
- El Modelo de Black-Scholes: Un cálculo matemático sobre acciones.
- La EDP de Black-Scholes (Ecuación Derivada Parcial): Esta ecuación rastrea el movimiento de una acción.
- La Fórmula de Black-Scholes: Intenta calcular los precios de las opciones de venta y compra (el derecho, pero no la obligación, de comprar una acción a un precio determinado antes de su fecha de vencimiento).
A menos que sea un matemático dedicado y empedernido, solo necesita saber cómo el trabajo de Black-Scholes podría afectar sus actividades de inversión. Si bien muchos expertos señalan las limitaciones de esta teoría, podría adoptar las predicciones y proyecciones que ofrecen los cálculos de Black-Scholes para optimizar su inversión en opciones.
La fórmula de Black-Scholes se utiliza para obtener el precio de las opciones europeas de compra y venta. Se obtiene resolviendo la EDP de Black-Scholes (véase la derivación a continuación).
Utilizando esta fórmula, el valor de una opción de compra en términos de los parámetros de Black-Scholes es:
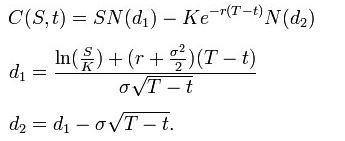
El precio de un put options es:
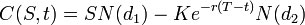
Para ambos, como arriba:
- N(•) es la función de distribución acumulada de la distribución normal estándar.
- T – t es el plazo de vencimiento.
- S es el precio al contado del activo subyacente.
- K es el precio de ejercicio.
- r es la tasa libre de riesgo (tasa anual, expresada en términos de capitalización continua).
- σ es la volatilidad de la rentabilidad logarítmica del activo subyacente.

