9-08 Tarification des options – Modèle Black-Scholes
Toute discussion sur les options et les prix des options serait incomplète sans une mention de la Black-Scholes modèle de tarification des options.
Les universitaires Fischer Black et Myron Scholes, dans un article qu’ils ont rédigé en 1973, ont exposé leur théorie selon laquelle une option était implicite dans la tarification de tout titre négocié.
En se référant aux travaux de certains des économistes les plus célèbres, comme Paul Samuelson, Black et Scholes ont développé non pas une, mais trois « positions » à considérer.
- Le modèle Black-Scholes : calcul mathématique relatif aux actions.
- L’équation aux dérivées partielles (EDP) de Black-Scholes : elle suit l’évolution d’une action.
- La formule Black-Scholes : elle tente de calculer les prix des options de vente et options d’achat .
À moins d’être un mathématicien acharné et invétéré, il vous suffit de savoir comment les travaux de Black-Scholes pourraient influencer vos activités d’investissement. Bien que de nombreux experts soulignent les limites de cette théorie, vous pouvez adopter les prédictions et projections proposées par les calculs de Black-Scholes pour faciliter vos activités d’investissement en options.
La formule de Black-Scholes permet d’obtenir le prix des options d’achat et de vente européennes. Elle est obtenue en résolvant l’équation aux dérivées partielles de Black-Scholes (voir la dérivation ci-dessous).
En utilisant cette formule, la valeur d’une option d’achat, en fonction des paramètres de Black-Scholes, est :
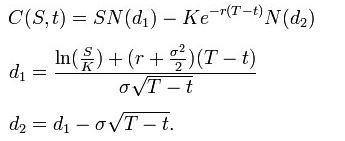
Le prix d’un options de vente est:
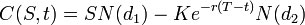
Pour les deux, comme ci-dessus :
- N(•) est la fonction de distribution cumulative de la distribution normale standard.
- T – t est la durée jusqu’à l’échéance.
- S est le prix au comptant de l’actif sous-jacent.
- K est le prix d’exercice
- r est le taux sans risque (taux annuel, exprimé en capitalisation continue)
- σ est la volatilité des rendements logarithmiques du sous-jacent

