Limites et journaux – Dépenses et épargne personnalisées
Une grande partie des finances personnelles repose sur une réflexion à long terme : établir son budget pour épargner suffisamment pour vivre le style de vie souhaité et vivre une retraite confortable.
Mais pour chaque individu, « vivre le style de vie souhaité » et « vivre une retraite confortable » peuvent avoir des significations très différentes. En fin de compte, chaque mois, chacun décide combien il va dépenser (ou consommer) et combien il va épargner (ou investir).
En comprenant le processus de réflexion derrière ce compromis, vous pouvez avoir une vision plus claire de vos propres dépenses. Cela vous aidera à vous assurer que vos dépenses réelles correspondent à vos dépenses prévues.
Modélisation de la consommation – Rendements d’échelle décroissants
Une grande partie des mathématiques financières se concentre sur la croissance exponentielle : comment un investissement croît en fonction d’un taux d’intérêt, comment un compte d’épargne croît au fil du temps ou comment se constituer un patrimoine à long terme. Les fonctions exponentielles ont une courbe ascendante : les investissements augmentent avec le temps.

Mais lorsque vous dépensez au lieu d’épargner, le bénéfice que vous obtenez pour chaque dollar dépensé ne suit pas cette courbe ascendante. Au contraire, les économistes affirment que la consommation a rendements d’échelle décroissants.
Imaginez : vous voyez deux appartements à louer. L’un comprend une chambre, l’électroménager a 30 ans, la salle de bain est minuscule et la cuisine n’a même pas la place d’une table. Cet appartement est affiché à 500 $ par mois.
Le deuxième appartement est équipé d’électroménagers neufs, d’une salle de bain spacieuse avec baignoire et douche séparées, et la cuisine est équipée de plans de travail en granit pouvant accueillir une table et un bar. Celui-ci est affiché à 1 500 $ par mois.
Le deuxième appartement pourrait bien valoir 1 000 $ de plus par mois. Mais la valeur ajoutée que vous obtenez en louant un appartement (un endroit où dormir, ranger vos affaires en toute sécurité, cuisiner et manger, etc.) est l’élément le plus important. Si vous essayez de décomposer tous les équipements offerts par l’appartement le plus cher pour déterminer la source de cette valeur, cela pourrait ressembler à ceci :
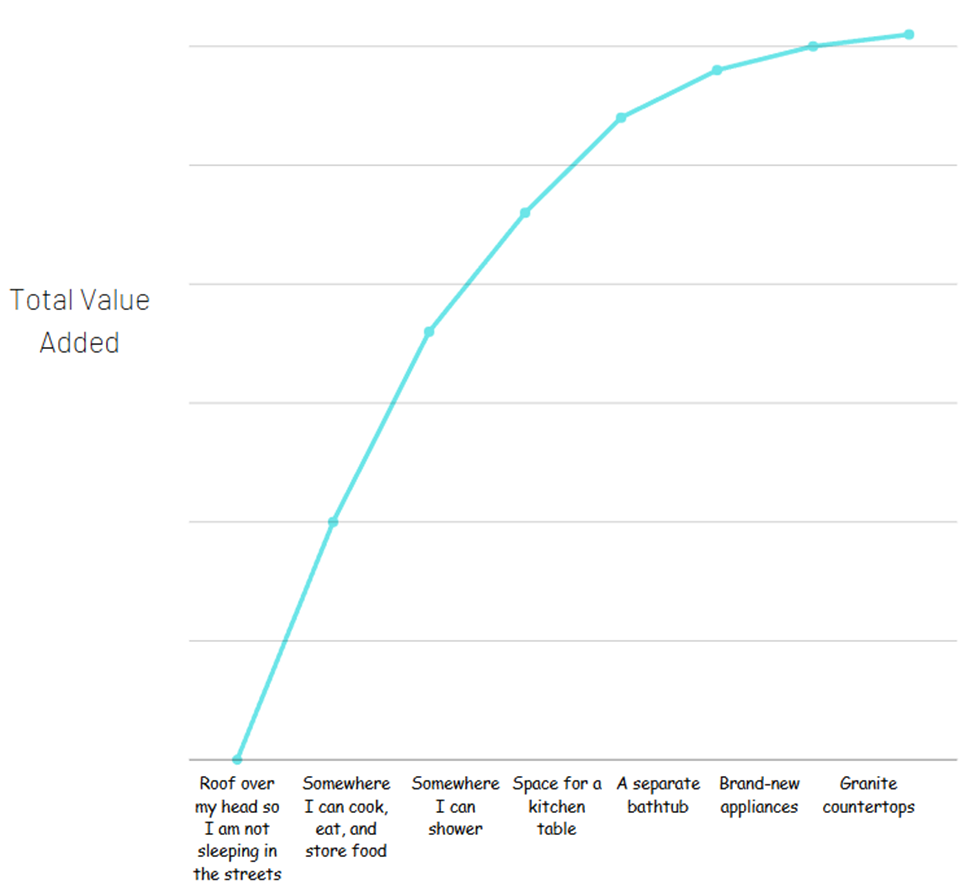
La majeure partie de la valeur totale provient des éléments de base. Cela ne signifie en aucun cas que les extras n’en valent pas la peine : il ne s’agit pas de dollars, mais simplement de la valeur obtenue.
En économie, ce concept est appelé utilité : la satisfaction ou le bénéfice tiré de la consommation de biens ou de services. Vous remarquerez que la courbe s’aplatit à mesure que les dépenses augmentent. Pour modéliser cela mathématiquement, nous utilisons des logarithmes plutôt que des exposants.
Qu’est-ce qu’un logarithme ?
On peut considérer les logarithmes par rapport aux exposants de la même manière que la division est liée à la multiplication : c’est la fonction mathématique inverse. Autrement dit,
Si 2^3 = 8, alors 3 est le logarithme de 8 en base 2.
En économie et en finance, les logarithmes sont utiles pour illustrer ces rendements d’échelle décroissants des dépenses. Par exemple, si nous souhaitons créer un graphique montrant l’utilité de la consommation au cours d’un mois donné, le graphique pourrait ressembler à ceci :
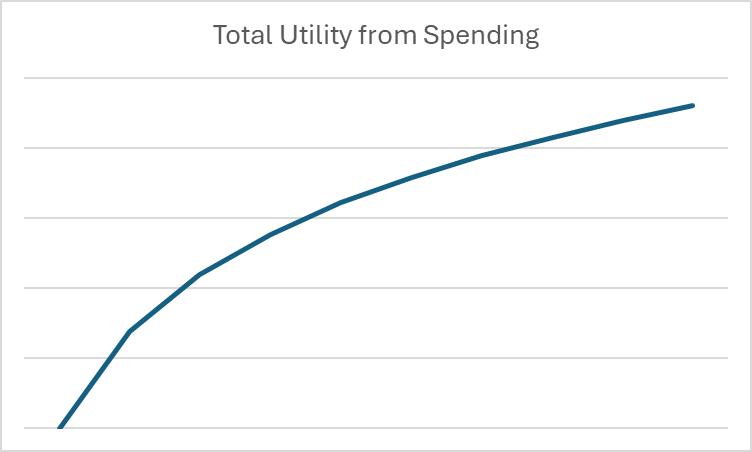
Une fois que nous avons placé nos dépenses dans le contexte des logarithmes et de l’utilité, nous pouvons commencer à considérer les décisions de dépenses et d’épargne à long terme uniquement en termes mathématiques.
Valeur temporelle de l’argent – Taux d’actualisation
La valeur temporelle de l’argent fait référence au fait qu’un dollar dans le futur vaut moins qu’un dollar aujourd’hui. En effet, entre maintenant et demain, j’aurais pu utiliser ce dollar pour faire quelque chose, et cette opportunité aurait pu être manquée.
Pour décrire mathématiquement la valeur temporelle de l’argent, nous utilisons ce qu’on appelle le taux d’actualisation. Ce taux est un nombre simple compris entre 0 et 1 qui répond à la question suivante :
À combien seriez-vous prêt à renoncer aujourd’hui pour obtenir 1 $ dans un mois ?

Le taux d’actualisation est différent pour chaque personne : il fait référence à ses préférences personnelles à court ou à long terme. Comme on peut s’y attendre, une personne avec un taux d’actualisation élevé (par exemple, 0,9) est beaucoup plus susceptible d’être épargnante qu’une personne avec un taux d’actualisation faible (par exemple, 0,3). En effet, une personne avec un taux d’actualisation faible attache une grande importance à avoir son argent immédiatement ; elle est donc prête à céder 70 % de sa valeur pour l’obtenir immédiatement plutôt que d’attendre.
Le taux d’actualisation est généralement exprimé par la lettre grecque β. Ainsi, si votre taux d’actualisation personnel est de 0,95, nous dirions β = 0,95.
Taux d’actualisation et exposants
Une fois que vous avez identifié votre taux d’actualisation personnel, vous pouvez également l’utiliser pour calculer le montant que vous accepteriez pour ce dollar dans un avenir encore plus lointain, en utilisant des exposants.
En augmentant votre bêta d’un exposant égal à l’horizon de calcul, nous pouvons déterminer la valeur actuelle de ce dollar. Autrement dit, β ^t = le montant que vous seriez prêt à accepter aujourd’hui en échange d’un dollar dans t mois.
Dans notre exemple, β = 0,95, voici la valeur d’un dollar dans un an :
| Mois dans le futur | Combien seriez-vous prêt à payer aujourd’hui pour sacrifier 1 $ dans le futur ? |
| 1 | $ 0.95 |
| 2 | $ 0.90 |
| 3 | $ 0.86 |
| 4 | $ 0.81 |
| 5 | $ 0.77 |
| 6 | $ 0.74 |
| 7 | $ 0.70 |
| 8 | $ 0.66 |
| 9 | $ 0.63 |
| 10 | $ 0.60 |
| 11 | $ 0.57 |
| 12 | $ 0.54 |
Cela signifie que si votre β = 0,95, vous seriez prêt à sacrifier 0,54 $ pour un dollar dans un an.
Maintenant que nous connaissons les concepts de logarithmes et de taux d’actualisation, nous pouvons les analyser pour comprendre leur impact sur les décisions d’épargne et de dépenses à long terme !
Utilitaire à vie
La majeure partie de ce que vous apprenez dans un cours de finances personnelles porte sur l’épargne pour l’avenir, notamment la retraite. Mais ce n’est pas vraiment votre objectif financier : vous cherchez avant tout à maximiser votre utilité totale tout au long de votre vie. C’est pourquoi personne n’économise chaque centime : vous cherchez à équilibrer l’avantage (ou l’utilité) de vos dépenses actuelles avec la croissance de votre patrimoine (grâce à la puissance des intérêts composés) pour pouvoir le dépenser plus tard.
Cela signifie que chaque mois de votre vie, vous disposez de vos revenus mensuels, auxquels s’ajoutent toutes les économies que vous avez accumulées jusqu’alors. C’est avec ces ressources combinées que vous devez travailler. Vous décidez consciemment de la part de ces ressources que vous dépenserez (ou consommerez) et de celle que vous épargnerez (ou investirez). Vous avez également une certaine compréhension du taux d’intérêt auquel votre épargne croîtra au fil du temps. En termes mathématiques, vous choisissez c et i où :
I + (s x (1 + r)) = c + i
Où ces variables font référence à :
- I = vos revenus mensuels
- s = le montant que vous avez déjà épargné/investi au début du mois
- r = le taux d’intérêt de croissance de votre épargne. Ainsi, votre épargne du mois dernier aura légèrement augmenté au début du mois par rapport au mois précédent.
- c = vos dépenses/consommations mensuelles
- i = le montant que vous épargnez/investissez ce mois-ci
Le bénéfice que vous tirez de votre consommation peut être exprimé en prenant le journal de votre consommation :
Utilitaire = log(c)
Vous devez déterminer combien dépenser (et donc épargner) à chaque période pour maximiser votre utilité totale sur toute votre vie, et pas seulement votre bonheur présent. À l’aide de votre taux d’actualisation et de vos exposants, nous pouvons calculer l’utilité que vous tirerez de votre consommation à n’importe quelle période future, puis additionner le tout.
Utilité totale à vie =
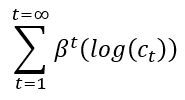
Limites – L’utilité et les remises approchent de zéro
À première vue, cela pourrait sembler infini – nous additionnons des nombres infinis, donc cela pourrait augmenter sans cesse. Cependant, comme t continue de croître, cela signifie que la réduction appliquée dans un avenir lointain commence à se rapprocher de zéro.
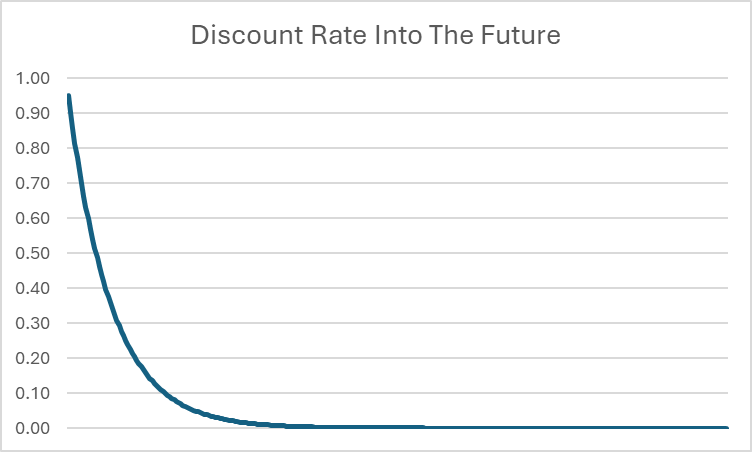
Par exemple, même si β = 0,95, le taux d’actualisation sur 20 ans descend jusqu’à 0,0000045. Plus on s’éloigne dans le futur, plus le taux d’actualisation se rapproche de 0. Bien que le montant maximal exact de consommation sur une vie soit impossible à calculer avec une précision absolue (car il pourrait théoriquement comporter un nombre infini de décimales), nous pouvons affirmer avec certitude qu’il existe une limite supérieure à la quantité totale de consommation atteignable sur une vie.
Des limites sont utilisées pour définir ces limites ascendantes et descendantes. On peut affirmer sans risque que le taux d’actualisation a une limite inférieure de 0 lorsque t croît vers l’infini ; il se rapprochera toujours de 0, mais ne l’atteindra jamais. La limite supérieure de l’utilité totale sur une vie peut également être calculée (mais cela nécessite des calculs avancés, qui ne font pas partie de ce cours).
Taux d’actualisation et taux d’intérêt : choisir d’épargner
Une fois que nous avons dépassé tous les calculs, ce que nous pouvons vraiment voir, c’est que la décision de dépenser ou d’épargner est basée en réalité sur seulement deux variables :
- Votre taux d’actualisation personnel (ou β)
- Le taux d’intérêt r, qui détermine la croissance de vos investissements
S’il y a deux personnes qui s’attendent au même retour sur investissement pour leur épargne, mais que nous observons que l’une est un gros épargnant et l’autre un gros dépensier, nous pouvons dire que l’épargnant a un β plus élevé que le dépensier – nous pouvons utiliser un nombre réel pour quantifier dans quelle mesure une personne est épargnante ou dépensière.

Une bonne compréhension des taux d’intérêt est essentielle à la littératie financière. Si votre seule option d’épargne est un compte d’épargne à faible taux d’intérêt (avec un rendement annuel de seulement 3 %, par exemple), vous serez moins susceptible de privilégier des objectifs d’épargne à long terme. En effet, vous pourriez ne pas saisir pleinement le potentiel d’investissements plus risqués et plus rentables comme la bourse.
En fin de compte, l’aspect le plus important de la littératie financière est de connaître les options d’investissement qui s’offrent à vous et de prendre des décisions éclairées en fonction de votre situation personnelle et de votre tolérance au risque.